Trapezoid Geometry with Unknown Variables

Geometry Level 3

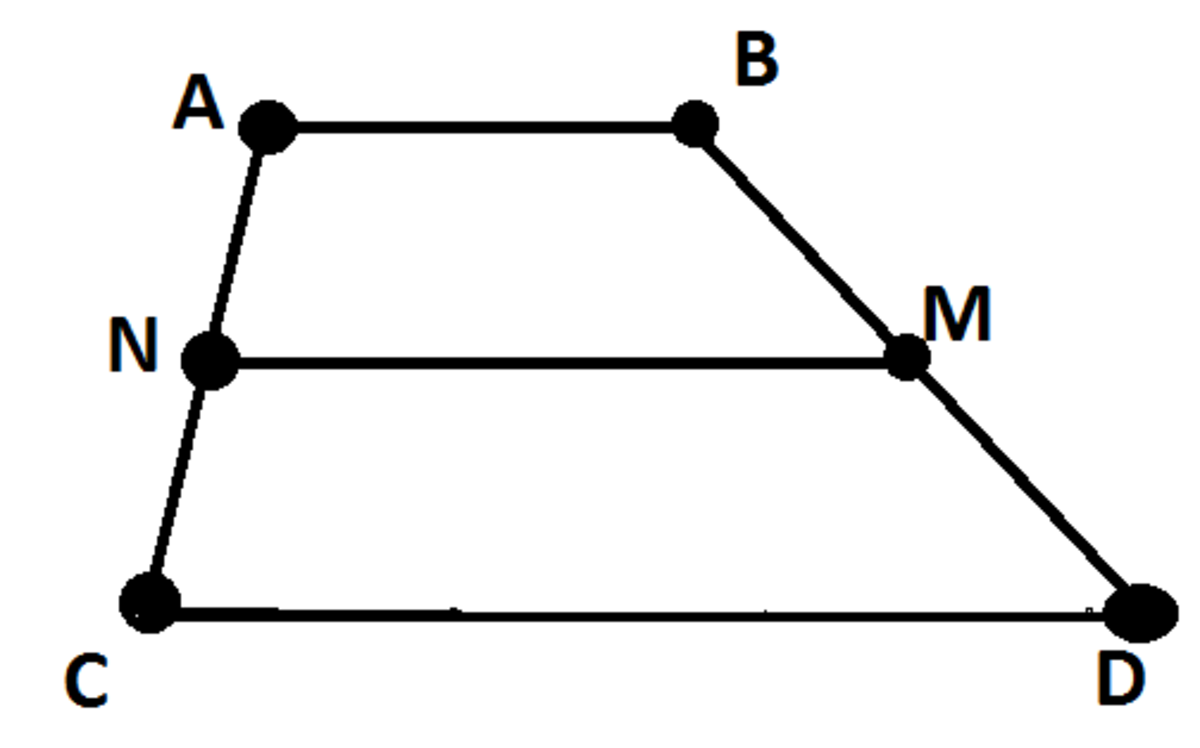
Line AB, NM, and CD are parallel to each other. Trapzeoid ABDC is cut into 2 different shapes (trapezoids with different dimensions) by line NM. Line AB is 1 unit long and Line CD is 7 units long. The height or angle measurements are not shown, nor what they measure to be in the picture. Figure ABMN and Figure NMDC have equal areas.

What is the length of Line NM?


The answer is 5.

Hasan Kunukcu by Hasan Kunukcu , 19, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Marta Reece
May 22, 2017

Areas

[ A B E ] = 1 2 × h × 1 = h 2 [ABE]=\frac12\times h\times1=\frac{h}{2}

[ N M E ] = 1 2 × x h × x = h x 2 2 [NME]=\frac12\times xh\times x=\frac{hx^2}{2}

[ D C E ] = 1 2 × 7 h × 7 = 49 h 2 [DCE]=\frac12\times 7h\times7=\frac{49h}{2}

[ A B M N ] = [ N M E ] − [ A B E ] = h x 2 2 − h 2 [ABMN]=[NME]-[ABE]= \frac{hx^2}{2}-\frac{h}{2}

[ D C M N ] = [ D C E ] − [ N M E ] = 49 h 2 − h x 2 2 [DCMN]=[DCE]-[NME]= \frac{49h}{2}-\frac{hx^2}{2}

Condition [ A B M N ] = [ D C M N ] [ABMN]=[DCMN] translates into an equation

h x 2 2 − h 2 = 49 h 2 − h x 2 2 \frac{hx^2}{2}-\frac{h}{2}=\frac{49h}{2}-\frac{hx^2}{2}

x 2 − 1 = 49 − x 2 x^2-1=49-x^2

x = 5 x=\boxed{5}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...