Trapezoid Made into 2 Kites
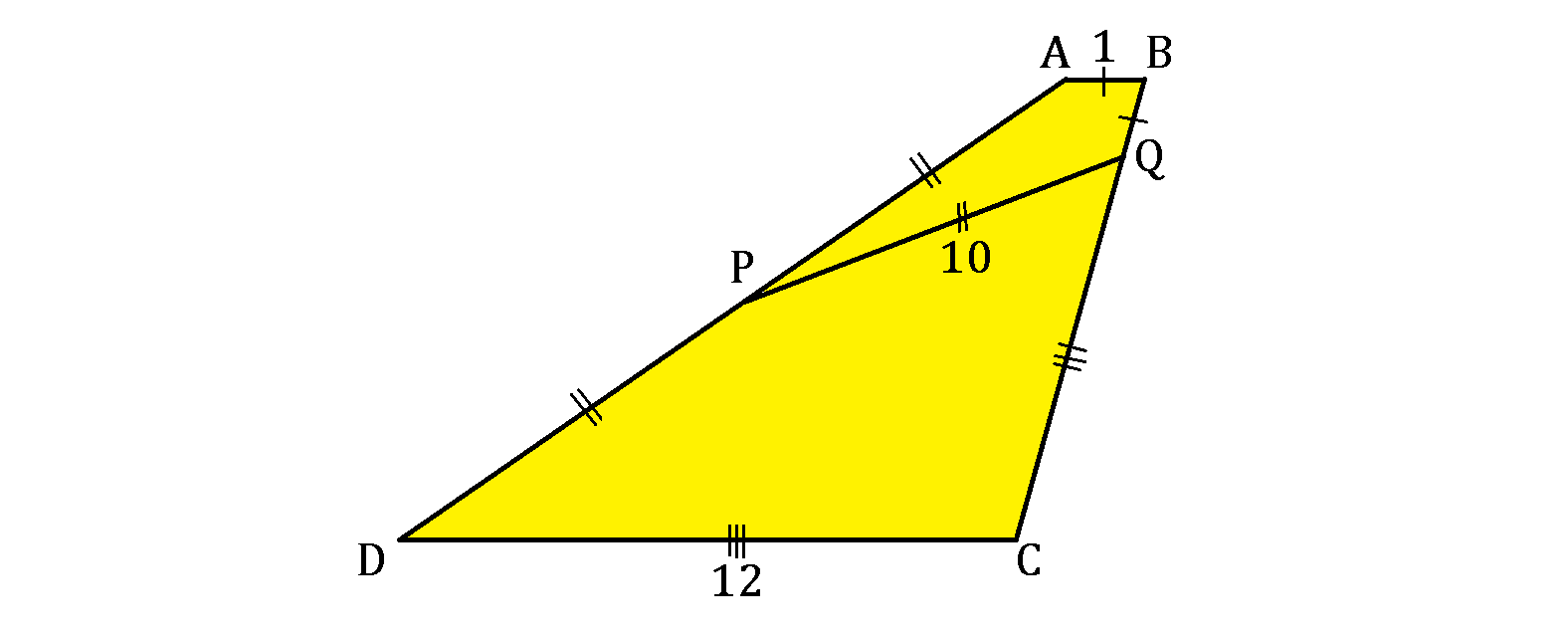
As shown above, A B C D is a trapezoid with A B ∣ ∣ C D , and then a line P Q is drawn such that it sections the trapezoid into 2 kites: A B P Q and P Q C D . The measured lengths include: A B = B Q = 1 ; P A = P D = P Q = 1 0 ; D C = C Q = 1 2 .
What is the area of the trapezoid A B C D ?
Note : Figure not drawn to scale
The answer is 78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
exquisite solution! @Brian Miyatake
First of all, let us duplicate the trapezoid image so that it forms a parallelogram with twice the area, as the following:
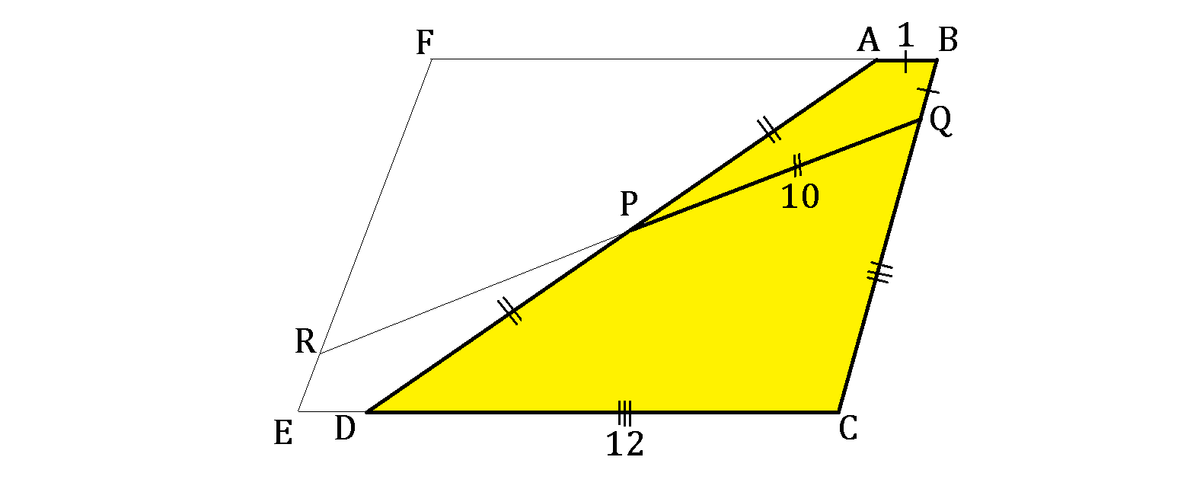
Obviously, we can observe that B C E F is not only a parallelogram, but also a rhombus because all four sides are congruent and the opposite sides are parallel. It is also natural to conclude that this rhombus has twice the area of the trapezoid, as the conventional formula of the trapezoid has portrayed.
Then we will join all the blue lines connecting the points R , D , A , Q and red diagonal lines, as shown below:
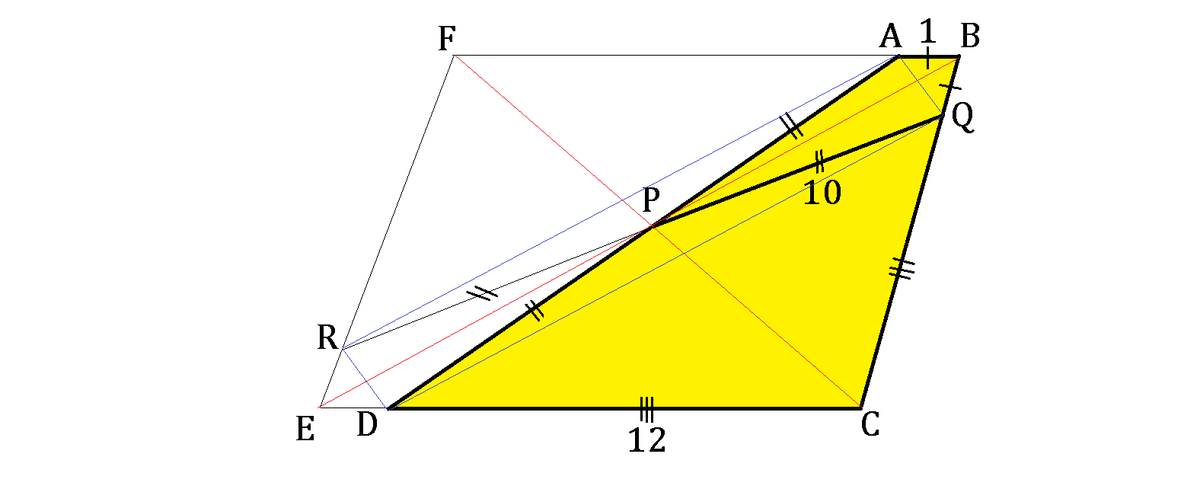
With triangles A B Q and R E D congruent by A B = B Q = R E = E D and ∠ A B Q = ∠ R E D by trapezoid tiling, we can also deduce that the triangles P R D and P A Q are also congruent because R D = A Q ; D P = P A ; a n d ∠ R P D = ∠ A P Q . Thus, R P = P D .
By similar methods, we could prove that R A = D Q and both diagonals R Q and D A intersect at their midpoints, making R A Q D a rectangle with point P as its centroid.
Then by having R F = F A and R E = A B , we can conclude that R A ∣ ∣ E B , and similarly, E B ∣ ∣ D Q , where E B passes point P , halving the rectangle R A Q D .
Thereby, we can prove triangles R E P and P B Q are congruent because R E = B Q , R P = P Q and ∠ R P E = ∠ B P Q . Thus, E P = P B . That means the point P is also the centroid of the rhombus.
Hence, another diagonal F C will intersect E B at this point P as the perpendicular bisectors, due to the properties of the rhombus.
Therefore, B P Q is a right triangle with half the area of the trapezoid because it is formed by halves of the adjacent kites.
Then let B P = x and P C = y . By Pythagorean theorem, x 2 + y 2 = ( 1 + 1 2 ) 2 = 1 6 9 .
Then by Stewart's theorem , 1 0 2 = 1 + 1 2 1 x 2 + 1 2 y 2 − 1 × 1 2 = 1 3 x 2 + 1 2 y 2 − 1 2
Substituting x 2 = 1 6 9 − y 2 , we will obtain:
1 0 2 = 1 3 1 6 9 − y 2 + 1 2 y 2 − 1 2 = 1 3 1 6 9 + 1 1 y 2 − 1 2
1 1 2 × 1 3 = 1 6 9 + 1 1 y 2
1 1 y 2 = 9 9 × 1 3
y 2 = 9 × 1 3
Then x 2 = 4 × 1 3 , and so x = 2 1 3 and y = 3 1 3 .
Finally, the area of the trapezoid A B C D = twice the area of the triangle B P C = 2 × 2 1 × 2 1 3 × 3 1 3 = 7 8 .
Bonus
When drawing the height of this trapezoid/rhombus, we will obtain the height of 1 2 and extended base of 5 as shown below:
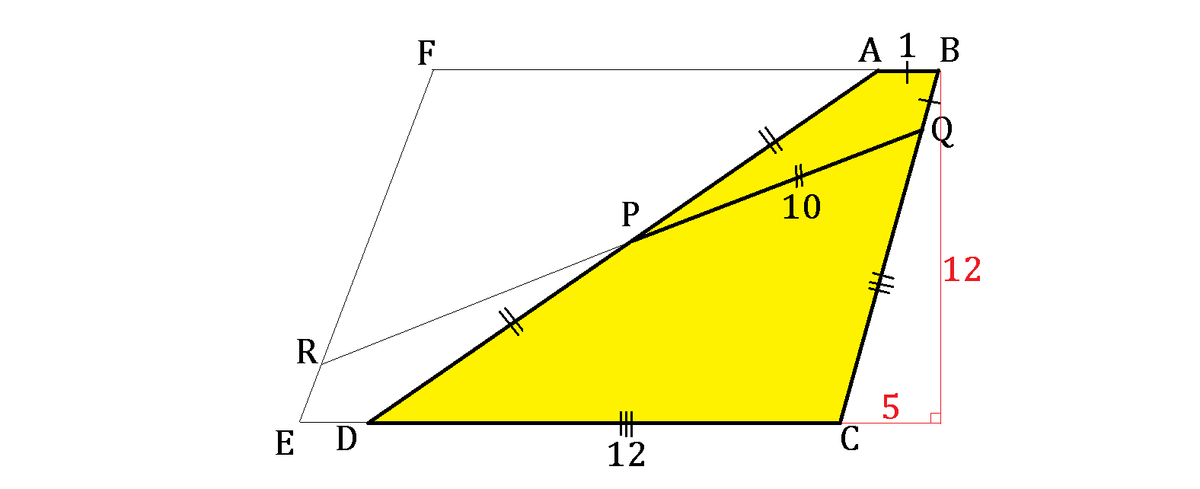
Draw segments A Q and D Q . Since P A = P Q = P D , they are all radii of a circle with center P and diameter A D , so by Thales' Theorem ∠ A Q D = 9 0 ° . Also drop the perpendicular from B to C D to meet at R .
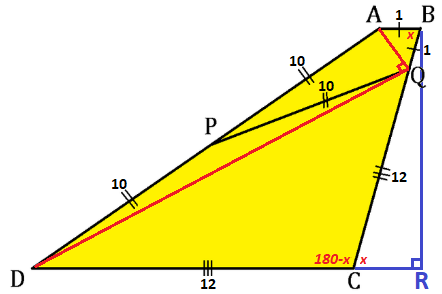
Let x = ∠ A B Q . Then since A B ∣ ∣ C D , ∠ B C D = 1 8 0 ° − x and ∠ B C R = x .
By the law of cosines on △ A B Q and △ C D Q , A Q 2 = 2 + 2 cos x and D Q 2 = 2 8 8 − 2 8 8 cos x .
By Pythagorean's Theorem on △ A D Q , 2 0 2 = 2 + 2 cos x + 2 8 8 − 2 8 8 cos x , which solves to cos x = 1 3 5 .
Since sin 2 x + cos 2 x = 1 and cos x = 1 3 5 , sin x = 1 3 1 2 . Then by solving △ B C R , B R = 1 2 , which is the height of the trapezoid.
The area of trapezoid A B C D is then A A B C D = 2 1 ( 1 2 + 1 ) 1 2 = 7 8 .
After you solved for cos x you could have directly solved for the height of the trapeziod.
The height of the trapezoid is given by 1 3 sin x ,from the triangle formed by dropping the perpendicular from B to D C produced.
Extend the line segments DA and CB, so that they meet at point O. Now, we have two similar triangles, OAB and OCD (as AB and CD are parallel, as they are the two bases of a trapezium).
The ratio of their side lengths is AB : CD = 1 : 12, therefore the ratio of their areas is 1 : 144, and the ratio of the area of the trapezium ABCD to the area of OCD triangle is 143 : 144.
Also, AD : OD = BC : OC = 11 : 12
Now, it is easy to calculate the side lengths of the OCD triangle:
O D = ( 1 0 + 1 0 ) ÷ 1 2 1 1 = 1 1 2 4 0
O C = ( 1 + 1 2 ) ÷ 1 2 1 1 = 1 1 1 5 6
C D = 1 2
At this point, we can calculate the area of the triangle either by calculating an angle by using the cosine rule and then applying the area formula, or from the side lengths directly, by using Heron's formula:
A △ A B C = s ( s − a ) ( s − b ) ( s − c ) , where s = 0 . 5 × ( a + b + c )
s = 0 . 5 × ( 1 1 1 5 6 + 1 1 2 4 0 + 1 2 ) = 2 4
A △ O C D = 2 4 ( 2 4 − 1 1 1 5 6 ) ( 2 4 − 1 1 2 4 0 ) ( 2 4 − 1 2 ) = 1 1 8 6 4
Hence:
A t r a p e z i u m A B C D = 1 1 8 6 4 × 1 4 4 1 4 3 = 7 8
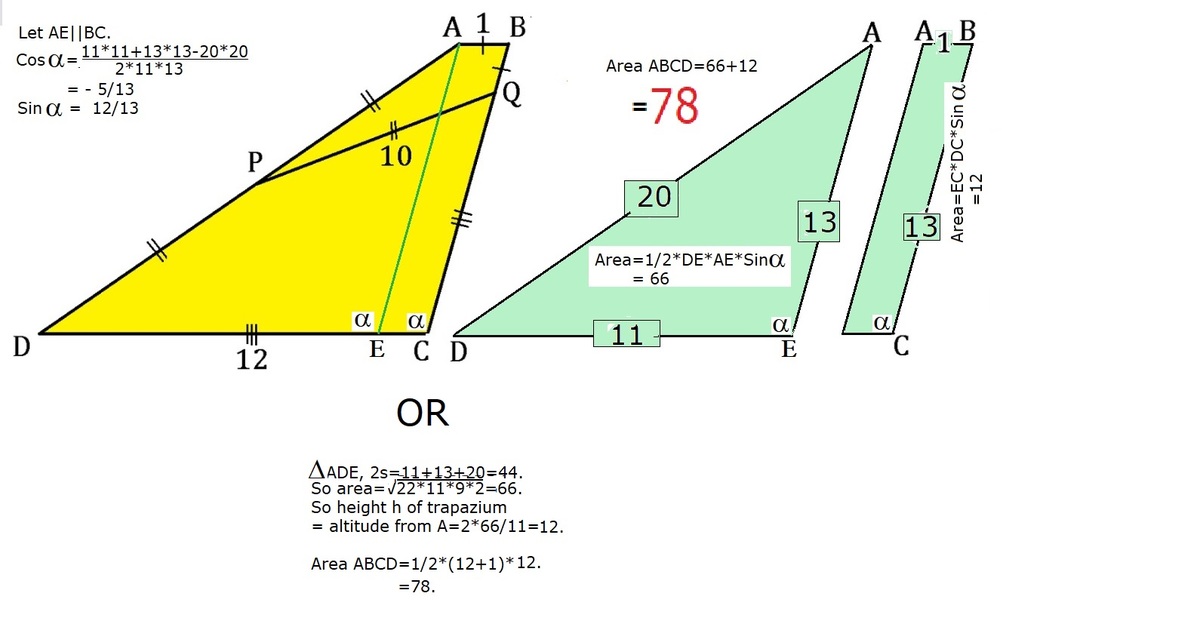
Draw point E so that segment A E ⊥ E D and draw point F so that B F ⊥ C F . Now let B F = E D = h . Then, because A D = 2 0 , E A = 4 0 0 − h 2 . Likewise, because C B = 1 3 , segment C F = 1 6 9 − h 2 . Since quadrilateral E B F D is a rectangle, it must be that E B = D F , or that 1 + 4 0 0 − h 2 = 1 2 + 1 6 9 − h 2 . Thus, h = 1 2 , and the area of the trapezoid is 2 1 2 + 1 ⋅ 1 2 = 7 8 .