Trapezoid, Parallelogram, & Triangle
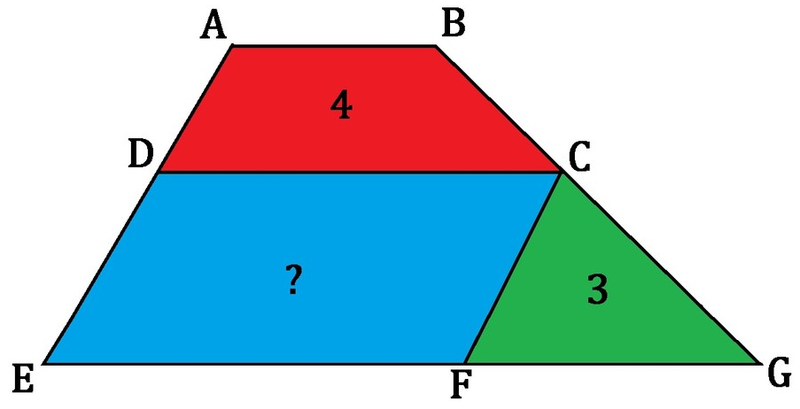
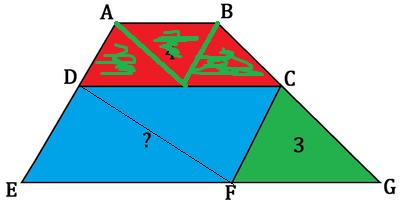
A trapezoid A B G E is partitioned into three smaller shapes: a trapezoid A B C D , a parallelogram C D E F , and a triangle C F G . The sides A B ∣ ∣ C D , and 2 A B = C D . The number in each colored region indicates the area of each shape.
What is the area of the blue parallelogram?
Note : Figure not drawn to scale.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
By Cavalieri's principle , we can reshape the big trapezoid A B C D into a right trapezoid while retaining all the same areas and parallel base lengths, as followed:
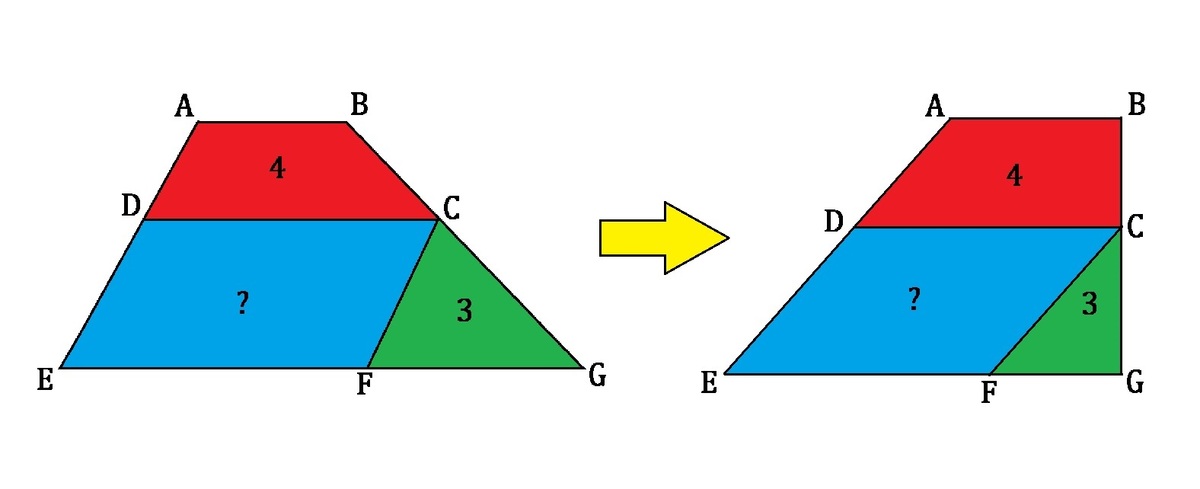
Now we will create a mirror image of such right trapezoid and join both shapes together to form a bigger isosceles trapezoid, as shown:
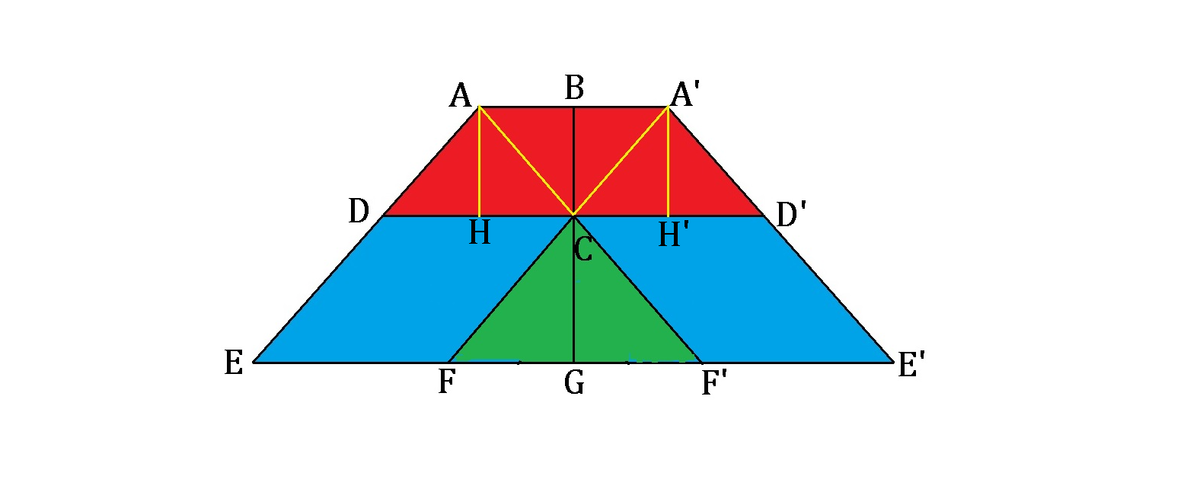
Then by drawing a line extending from F C to A ′ , it is clear that D A ∣ ∣ C A ′ and A A ′ = 2 A B = C D . Thus, A D C A ′ is also a parallelogram.
Furthermore, by drawing a line A H perpendicular to D C , we can see that D H = D C − H C = D C − A B = A B . Thus, A H bisects D C , and A D C is an isosceles triangle and has an area of 3 2 of the trapezoid A B C D , yielding 3 2 × 4 = 3 8 . The area of A D C A ′ is twice that of the isosceles triangle = 3 1 6 .
On the other hand, with A A ′ ∣ ∣ F F ′ and A F ′ intersecting F A ′ , we can conclude that △ A C A ′ ∼ △ F C F ′ . Then the area of △ F C F ′ is twice that of △ F C G , resulting in 6 . Thus, the area ratio of △ A C A ′ : △ F C F ′ = 3 8 : 6 = 4 : 9 = 2 2 : 3 2 .
Hence, it is obvious that the height ratio B C : C G = 2 : 3 .
Finally, since the parallelograms D C E F and A D C A ′ have the same base, we can calculate the desired area of D C E F by using such ratio: 3 1 6 × 2 3 = 8 .
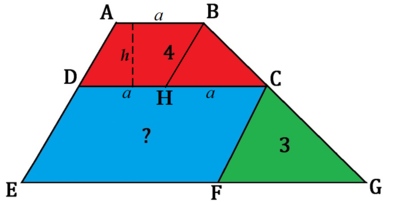 Let
A
B
=
a
and the height of trapezoid
A
B
C
D
be
h
. Draw a line
B
H
parallel to
A
E
to form parallelogram
A
B
H
D
. Then
D
H
=
H
C
=
a
.
Let
A
B
=
a
and the height of trapezoid
A
B
C
D
be
h
. Draw a line
B
H
parallel to
A
E
to form parallelogram
A
B
H
D
. Then
D
H
=
H
C
=
a
.
The area of trapezoid A B C D , [ A B C D ] = 2 a + 2 a h = 2 3 a h = 4 . ⟹ a h = 3 8 . Then the area of △ B C H , [ B C H ] = 2 1 a h = 3 4 .
We note that △ C F G is similar to △ B C H , Then the area of the two triangles are directly proportional to the square of the linear dimension. That is H C 2 F G 2 = [ B C H ] [ C F G ] = 3 4 3 = 4 9 , ⟹ F G = 2 3 a . Then the height of △ C F G , h ′ = 2 3 h , which is also the height of blue parallelogram C D E F .
Therefore, the area of the blue parallelogram [ C D E F ] = 2 a h ′ = 2 a × 2 3 h = 3 a h = 3 × 3 8 = 8 .
If we take a similar triangle to the Green one, we can fit 3 of them inside the Red trapezium. They each have area 3 4 and F G : A B = 3 : 3 4 = 3 : 2 .
Treating Blue as 2 triangles: the ratio of Blue to Green is 2 E F : F G = 4 : 2 3 = 8 : 3 . Hence the area of Blue is 8.
Extend FC to H, where H lies on the extension of AB. Let K be on BH and L be on Fg so that KL is a straight line perpendicular to BH and FG and passing through C. Let KC = d and CL = k. Then triangle BHC is similar to triangle FCG by 3 angles equal. Then d/x = h/y, and hx = dy. Area of triangle FCG = 3 = yh/2. So hy = 6, h(hx/d) = 6, (h^2)x = 6d, (h^2)(x^2) = 6dx. From trapezoid ABCD, Area = 4 =(1/2)(d)(x + 2x), or 8 = 3dx, and 16 = 6dx. But 6dx = (h^2)(x^2), so hx = 4. Finally, area of parallelogram CDEF = ? = ((1/2)(h)(4x) = (1/2)(4/x)(4x) =16x/2x = 8.
Extend A E and B G to meet at H .
△ A H B is similar to △ H D C by AA similarity, and since 2 A B = C D , 2 2 1 2 = A △ A H B + 4 A △ A H B , which solves to A △ A H B = 3 4 .
Using A △ = 2 1 b h , the height of △ A H B solves to h △ A H B = 3 A B 8 .
△ A H B is also similar to △ C F G by AA similarity, so h △ C F G 2 ( 3 A B 8 ) 2 = 3 3 4 , which solves to h △ C F G = A B 4 .
The area of the blue parallelogram is therefore A C D E F = C D ⋅ h △ C F G = 2 A B ⋅ A B 4 = 8 .