Trapezoid Riddle II
A right trapezoid is partitioned into 4 triangles by its diagonals, as shown below:
Which colored region has a larger area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Moderator note:
Overlapping triangles are a powerful technique but can be difficult to spot, particularly in a diagram like this one where the coloring strongly suggests each triangle be treated as an individual unit.
More problems with this type of trick (and many more besides) are at our Outside the Box Geometry exploration.
Very nice! Adding that white triangle to show that they are equal!
Could you please change [ B E D ] for [ B E C ] ?
I'm confused, how is [BCD] equal to 1/2hb?
Log in to reply
BCD is a triangle of height h and base b, hence its area is 1/2hb (base times height divided by two).
Log in to reply
Thanks Renan! I had worked out my obvious mistake about 5 minutes after posting (and my morning coffee :))
Oh ignore me - brain fade this morning!
Outstanding!
If C approches to D so that [ADC] and [BDC] are almost reduced to a line, line BC (hypotenuse) is always longer than the vertical side of the quasi rigtht triangle. So Red triangle will be larger. If the trapezoid was a rectangle (i.e. AD = BC), both triangles will be the same. Likewise, if C is extended to infinity, E will coincide with B, to form a finite triangle (ADB), whereas the red triangle BEC will have an infinite side. So, only when BC is vertical to DC, that is we have a regular rectangle, both triangles are equal.
Very good solution! Really easy to see and understand :).
Including the bottom white triangle, both triangles (white + blue and white + red) share the same base and same height.
This seems to be the easiest explanation.
There has to be an easy solution and this is it.
Simplicity rules the day!
Relevant wiki: Crossed Ladders Problem
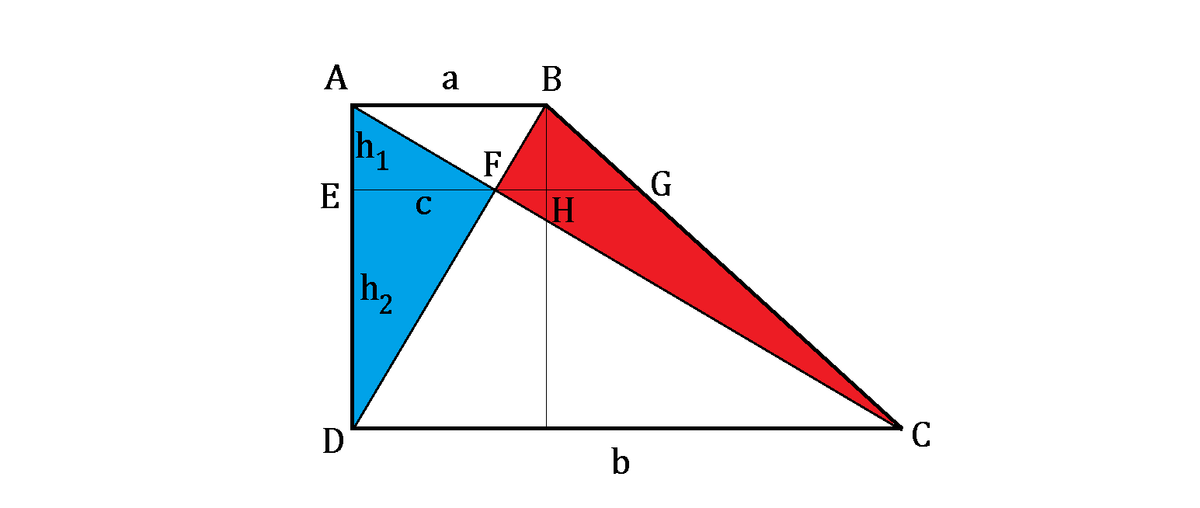
Let us denote the vertices and lengths as shown above, and E G / / A B / / C D and passes the intersection point F . According to Crossed Ladders Theorem , c 1 = a 1 + b 1 or c = a + b a b .
Then we are attempting to prove that c is, in fact, half the Harmonic Mean of a and b or, namely, that E F = F G .
By drawing a perpendicular line to E G with intersection at point H , suppose H G = x .
Then by similarity, h 1 + h 2 b − a = h 1 x and h 1 c = h 1 + h 2 b .
Thus, h 1 h 1 + h 2 = c b = x b − a .
x = b c ( b − a ) = c − b a c = c − a + b a 2 .
Now since a − c = a − a + b a b = a + b a 2 , x = c − ( a − c ) = 2 c − a .
Thus, E G = a + x = 2 c . Hence, F G = c = E F .
As a result, since both △ A E F and △ B F G share the same height and base length, they have the same area.
Similarly, since both △ E F D and △ G F C share the same height and base length, they have the same area.
Finally, that concludes that both red and blue triangles have the same area.
Note : That also proves that the length of E G is the harmonic mean of a and b .
If you slide B closer and closer to A, obviously both areas are equal; they are both zero. If you slide B to above C so that it forms a rectangle, obviously both areas are again equal. Since sliding is a linear operation on the ratio, they are always equal
As △ A C D and △ B D C have same altitude and basis: A r e a ( △ A C D ) = A r e a ( △ B D C ) As blue area is: A r e a ( △ A C D ) − A r e a ( △ E D C ) = A r e a ( △ B D C ) − A r e a ( △ E D C ) We find: B l u e A r e a = R e d A r e a
You can solve this question by applying Cavalieri's principle. You can create an isosceles trapezoid with same height and base lengths. By symmetry you have that both areas are equal. But also, applying Cavalieri's principle, the triangles of the problem must have the same area of their respective symmetric triangles. Therefore the areas are equal.
Oh, this is an unexpected approach! Thanks for sharing!
Triangle ABD and triangle CBA are at the same base AB and between the same parallels AB and DC. So their areas are equal.
Now, Euclid's axiom states that when equals are subtracted from equals, the results are also equal.
So, area of triangle ABD-area of triangle ABE=area of triangle ABC-area of triangle ABE
Or area of triangle AED=area of triangle BEC
Like it ... intuitive
I thought of the right trapeziod as being part of a rectangle with a corner missing. I know that if the red and blue areas were in a rectangle, their areas would be identical. Now say we begin reducing the length of the top line of the rectangle slowly to the left, (forming a right trapezoid). We continue to shorten the top line of the trapezoid until we have a right triangle, at which point both the red and blue areas would disappear simultaneously. I interpolated that neither colored area could be larger than the other anywhere along the way.
You could also solve using similar triangles. notice that triangles AEB and CED are similar.
∴ E C A E = E D E B = (say) α . Now A E = α E C and E B = α E D .
Therefore it's easy to see that area of triangle AED = area of Triangle BEC
(for the area you can the formula use Area=
(
1
/
2
)
a
b
sin
(
θ
)
)
.
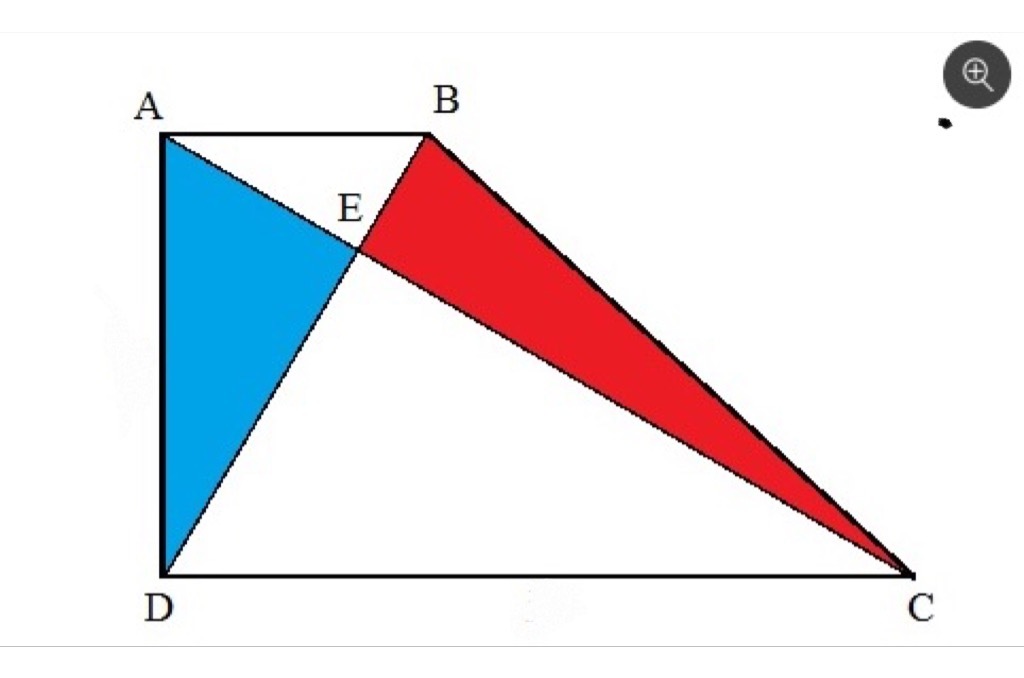
The area of a triangle can be computed as the product of the lengths of two legs and the sin of the angle between them. Taking the center vertex, the opposite angles on the left and right are the same. The correspondingly adjacent legs of the red and blue triangles have equal products since the white triangles are similar.
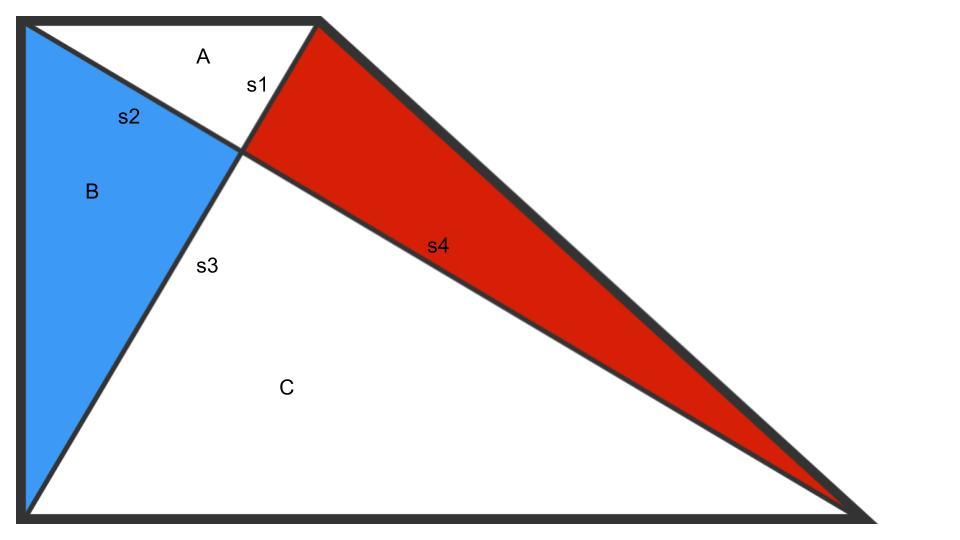
Triangles A, B, and C are similar right triangles.
Therefore s 2 s 1 = s 3 s 2 = s 4 s 3 Therefore s2 s3 = s1 s4, and the red and blue triangles have the same area.
But this assumes the diagonals intersect at rightangles. Why is this obvious?
This is how I did it. Sort of: I used proportions If s2=s1(x), where x is the fixed proportion. s3=s1(x)^2 s4=s1(x)^3 Ared = 1/2(s1(x^2))(s1(x)) Ablue = 1/2(s1(x^3))(s1) Which are the same. It doesn't matter whether or not the inner triangles are 'right' at the intersection, it's only comparing similarity.
Here's how I did it: Let b 1 = length of top base Let b 2 = length of bottom base Let h = height of trapezoid Let B = area of Blue triangle Let R = area of Red triangle Let S = area of Small white triangle Let L = area of Large white triangle
I know the area of the bigger right triangle (the one made up of the Blue triangle and Large white triangle) is: 2 1 b 2 h
I also know the area of the smaller right triangle (the one made up of the Blue triangle and the Small white triangle) is 2 1 b 1 h
Thus, ( 1 . ) B + L = 2 1 b 2 h ( 2 . ) B + S = 2 1 b 1 h
Using the area formula of a trapezoid, I know: Total Area = 2 1 h ( b 1 + b 2 )
Using the distributive and commutative properties, I can modify this:
Total Area = 2 1 b 1 h + 2 1 b 2 h
Using substitution from equations (1.) and (2.) above, I can conclude:
Total Area = B + L + B + S and thus by simplifying the right side:
( 3 . ) Total Area = 2 B + L + S
I also know that the Total Area equals the sum of the areas of the 4 triangles, thus:
Total Area = B + R + L + S
Using substitution from equation (3.) above, you get:
B + R + L + S = 2 B + L + S
So if you subtract "L" and "S" from both sides, you get:
B + R = 2 B
So now you can subtract "B" from both sides and you get:
R = B
This proves that area of the Red triangle is equal to the area of the Blue triangle. :)
Yup, this is how I solved this question. Who knew that setting up a bunch of symbols and equations can simplify the whole thing?
Simple,make AB=DC. You now have a rectangle, so the 4 triangles formed by the crossing diagonals are obviously equal. Note: The definition of "right trapezoid" is fuzzy. Either "a trapezoid with two right angles" or "at least two right angles". If one insists on applying the first definition, simply make DC=AB+ delta, with delta approaching zero.
Why must AB=DC be true? I don't see how that must be the case...
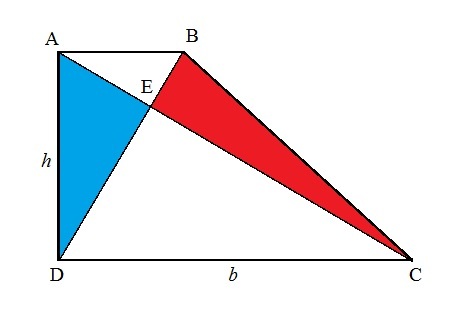
Let the height of the right trapeziod A D = h and its base C D = b , the area of blue region [ A E D ] = A b l u e and that of red region be [ B E C ] = A r e d . We note that:
[ A C D ] [ B C D ] ⟹ [ A C D ] [ A E D ] + [ E C D ] A b l u e = 2 1 h b = 2 1 h b = [ B C D ] = [ B E C ] + [ E C D ] = A r e d
⟹ Both are equal.