Trapezoid Riddle
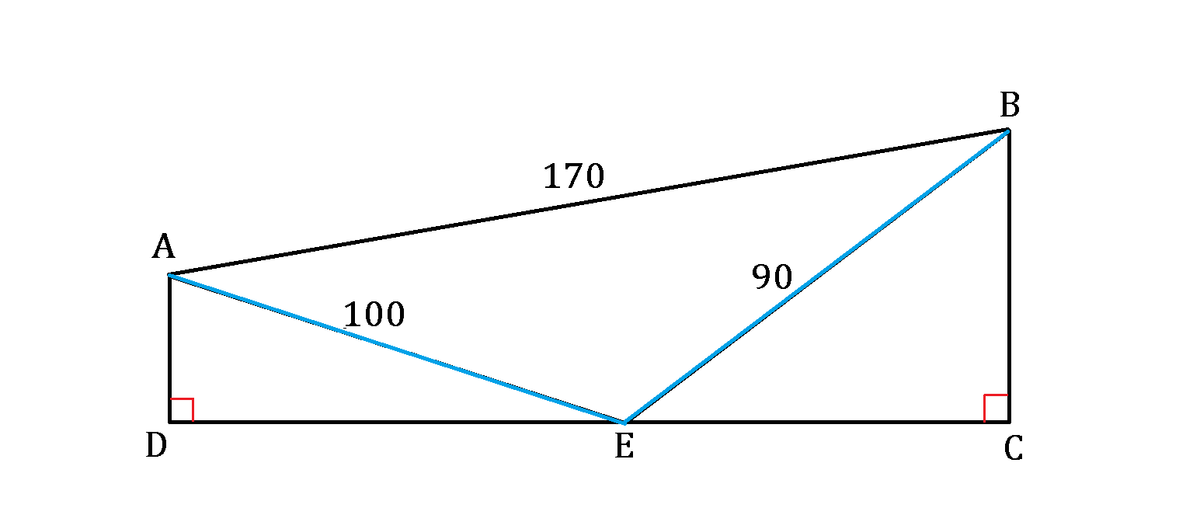
Trapezoid A B C D has ∠ C = ∠ D = 9 0 ∘ and A B = 1 7 0 with A D ∣ ∣ B C , as shown above. Point E is picked on D C such that A E = 1 0 0 and B E = 9 0 . All of the segments A D , D E , E C , and C B have integer lengths.
What is the perimeter of trapezoid A B C D ?
The answer is 420.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
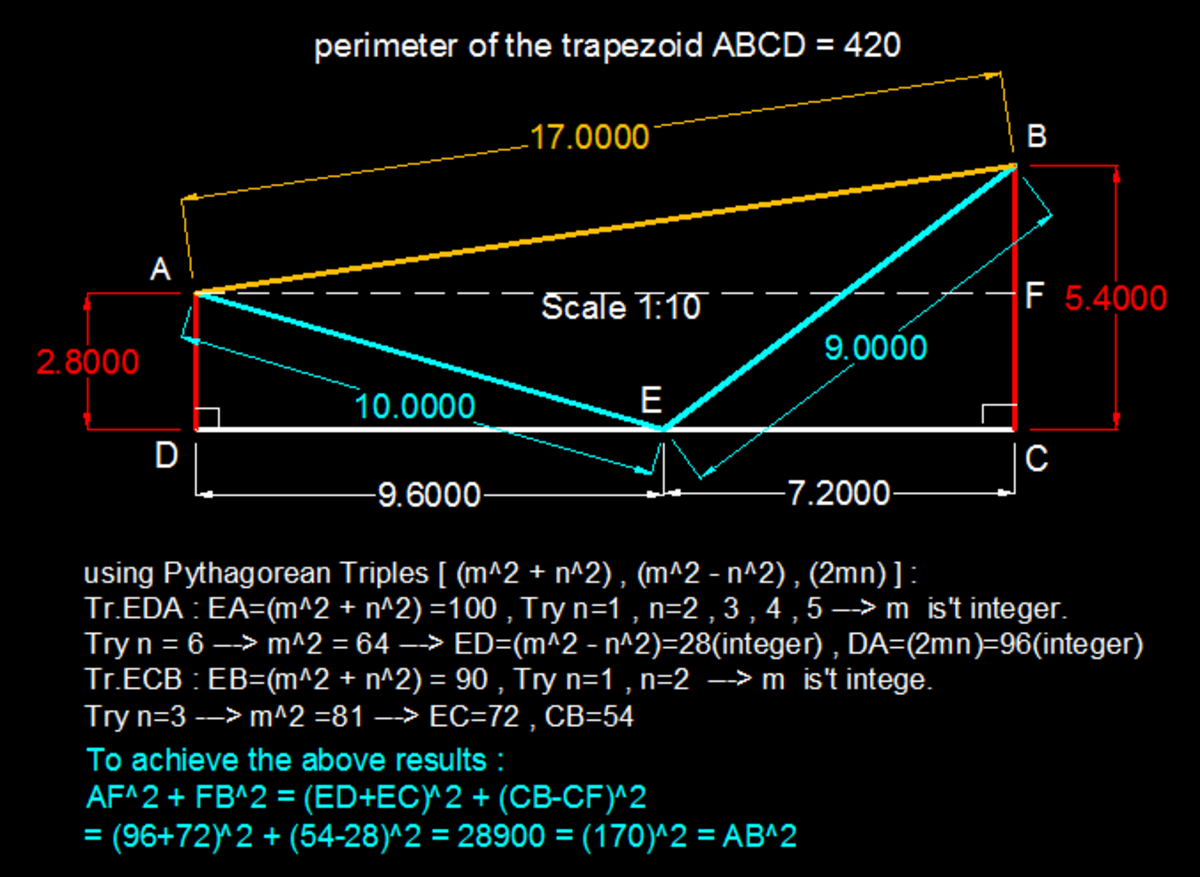
sir why is this wrong, AD=60, DE=80, EC=72, BC=54. Most likely I am wrong
Log in to reply
AD=60 , BE=80 achieved the phythagorean triple of triangle ADE only. But the problem required to achievealso the phythagorean triple of triangle AEF such that :
AB^2 = BF^2 + AF^2 ---> (170)^2 = (BC-CF)^2 + (CE+ED)^2
I used a similar approach, however to be complete you need to show that the solution is unique. For this I took the list of pythagorean triangles with hyp 100 which is simply (28,96) and (60,80). Then I did the same for hyp 90 which is strictly (54,72). Thus there are only two combinations to check using the length of AB, namely the combinations of (28,96),(54,72) and (60,80),(54,72) and only (28,96),(54,72) results in AB having the proper length of 170. Thus this solution is unique.
B y C o s R u l e i n Δ A E B , ∠ A E B = C o s − 1 2 ∗ 1 0 0 ∗ 9 0 1 0 0 2 + 9 0 2 − 1 7 0 2 = 1 2 6 . 8 7 o . W e h a v e P y t h a g o r e a n t r i p l e s : − 1 0 0 2 = 6 0 2 + 8 0 2 , o r 2 8 2 + 9 6 2 , . . . . a n d . . . . . . 9 0 2 = 5 4 2 + 7 2 2 . C o r r e s p o n d i n g a n g l e s h y p o t e n u s e m a k e s w i t h l e g s a r e , C o s − 1 1 0 0 6 0 = ( 5 3 . 1 3 o , 3 6 . 8 7 o ) ; o r C o s − 1 1 0 0 2 8 = ( 7 3 . 7 4 o , 1 6 . 2 6 o ) , . . . . . . . . . . a n d . . . . . . C o s − 1 9 0 5 4 = ( 5 3 . 1 3 o , 3 6 . 8 7 o ) . H o w e v e r C o s − 1 1 0 0 6 0 = C o s − 1 9 0 5 4 , a n d s o ( 7 3 . 7 4 o , 1 6 . 2 6 o ) , a n d ( 5 3 . 1 3 o , 3 6 . 8 7 o ) , o n l y t o b e i n v e s t i g a t e d . ∠ D E C = 1 8 0 o = ∠ D E A + ∠ A E B + ∠ B E C = ∠ D E A + 1 2 6 . 8 7 + ∠ B E C . ∴ ∠ D E A + ∠ B E C = 5 5 . 1 3 o , H e n c e ∠ B E C = 3 6 . 8 7 o . C a n n o t b e 5 3 . 1 3 , s i n c e t h a t l e a v e s ∠ D E A = 2 o o n l y . S o ∠ D E A m u s t b e 5 5 . 1 3 o − 3 6 . 8 7 o = 1 6 . 2 6 , a n d t h a t i s w h a t w e h a v e . S o t h e p e r i m e t e r o f t r a p e z o i d = L e g s o f Δ s ( A D E + B E C ) + 1 7 0 = 2 8 + 9 6 + 5 4 + 7 2 + 1 7 0 = 4 2 0 .