Trapezoid problem
Given Trapezoid
A
B
C
D
as shown.
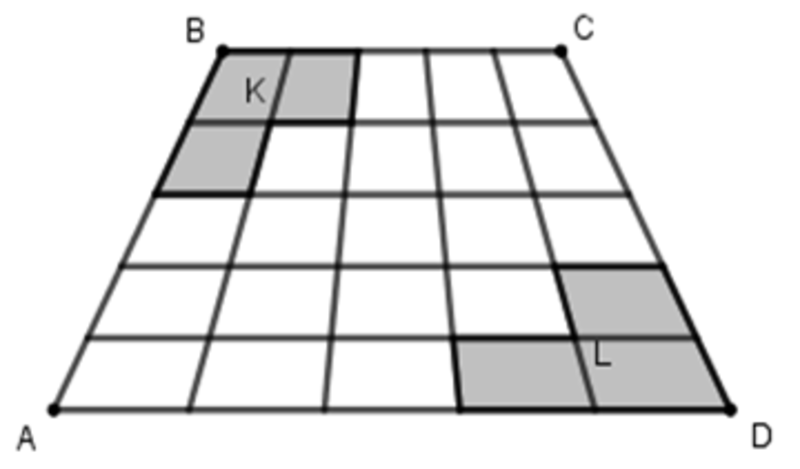
The trapezoid is divided into 5 parts horizontally with A B and C D are equally divided. The Trapezoid also divided into 5 parts vertically with A D and B C are devided equally. If the shaded regions K has area 3 5 and the shaded region has area 5 5 . Determine the area of the trapezoid A B C D .
The answer is 375.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let ∣ B C ∣ = a , ∣ A D ∣ = b and the height of the trapezoid be h . Then 2 × 2 1 × ( 5 a + 2 5 4 a + b ) × 5 h + 2 1 × ( 2 5 4 a + b + 2 5 3 a + 2 b ) × 5 h = 3 5 or h = 5 ( 5 a + b ) 2 5 0 × 3 5 . And 2 × 2 1 × ( 5 b + 2 5 a + 4 b ) × 5 h + 2 1 × ( 2 5 a + 4 b + 2 5 2 a + 3 b ) × 5 h = 5 5 or h = 5 ( a + 5 b ) 2 5 0 × 5 5 . Therefore a = 2 b , h = b 5 0 0 and the required area is 2 1 ( a + b ) h = 3 7 5
Same way (just about). One point - you may not want to edit this now that you've posted, but the formulas work out much neater if you let B C = 1 0 a , A D = 1 0 b - this eliminates almost all of the fractions. Also, once you get h ( 5 a + b ) = 1 7 5 0 and h ( a + 5 b ) = 2 7 5 0 (in your original notation), you can just add these up to get 6 h ( a + b ) = 4 5 0 0 .
Let B C = a and A D = b . If we label the four horizontal division lines be B n C n , where n = 1 , 2 , 3 , 4 , and the length B n C n = a n . Then a n = a + 5 n ( b − a ) . Let the height of the trapezoid be h . Then we have:
2 ( 2 5 a + 5 a 1 × 5 h ) + ( 2 5 a 1 + 5 a 2 × 5 h ) 1 2 5 ( 9 a + b ) h + 2 5 0 ( 7 a + 3 b ) h ⟹ ( 5 a + b ) h = 3 5 = 3 5 = 1 7 5 0 . . . ( 1 )
Similarly,
( 2 5 a 3 + 5 a 4 × 5 h ) + 2 ( 2 5 a 4 + 5 b × 5 h ) 2 5 0 ( 3 a + 7 b ) h + 1 2 5 ( a + 9 b ) h ⟹ ( a + 5 b ) h = 5 5 = 5 5 = 2 7 5 0 . . . ( 2 )
From ( 1 ) + ( 2 ) : 6 ( a + b ) h = 4 5 0 0 , then the area of the trapezoid 2 ( a + b ) h = 1 2 4 5 0 0 = 3 7 5 .