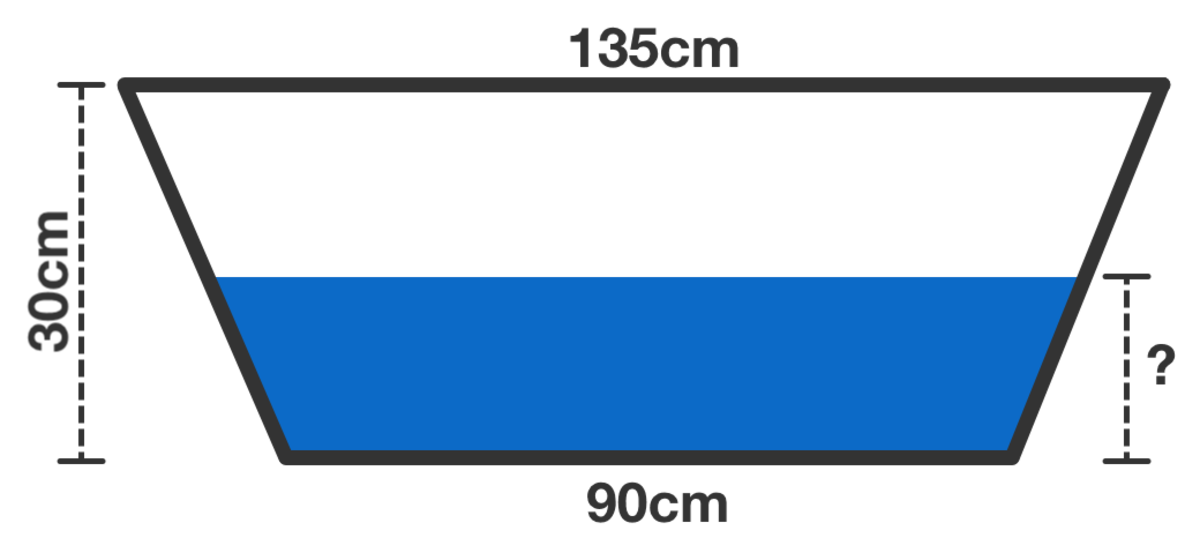
Trapezoidal Tank

Let the height of the water be $h$ cm and the width of the water surface be $w$ cm. The the volume of water in the trapezoidal tank $V = \dfrac {(w+90)h}2 \times 1$ . And we note that $w=\dfrac {135-90}{30}h + 90 = \dfrac 32 h+90$ . Then, we have:

$\begin{aligned} V & = \frac {(w+90)h}2 = \frac {\frac 32 h^2 + 180h}2 & \small \color{#3D99F6} \text{Putting }V = 1188 \\ \implies \frac {3h^2 + 360h}4 & = 1188 \\ h^2 + 120h - 1584 & = 0 \\ (h-12)(h+132) & = 0 \\ \implies h & = \boxed{12} & \small \color{#3D99F6} \text{Note that }h > 0 \end{aligned}$

The water can be separated into two parts: a rectangle $90$ by $h$ , and two halves of a triangle with a height:width ratio of $30:45$ , and height $h$ . This means the width of the triangle is $\frac{45}{30}\times h$ .

From this, we can get the equation for the total volume of water: $90h + \frac{45}{30}\times h \times \frac{h}{2} = 1188$ .

This can be rearranged to $\frac{3}{4}h^2+90h=1188$ , and with this, we can complete the square to find $h$ :

$h^2+120h=1584$

$h^2+120h+60^2=1584+3600=5184$

$(h+60)^2=5184$

$h+60=72$

$h=\boxed{12}$ .