Trapezoids and Hexagons !
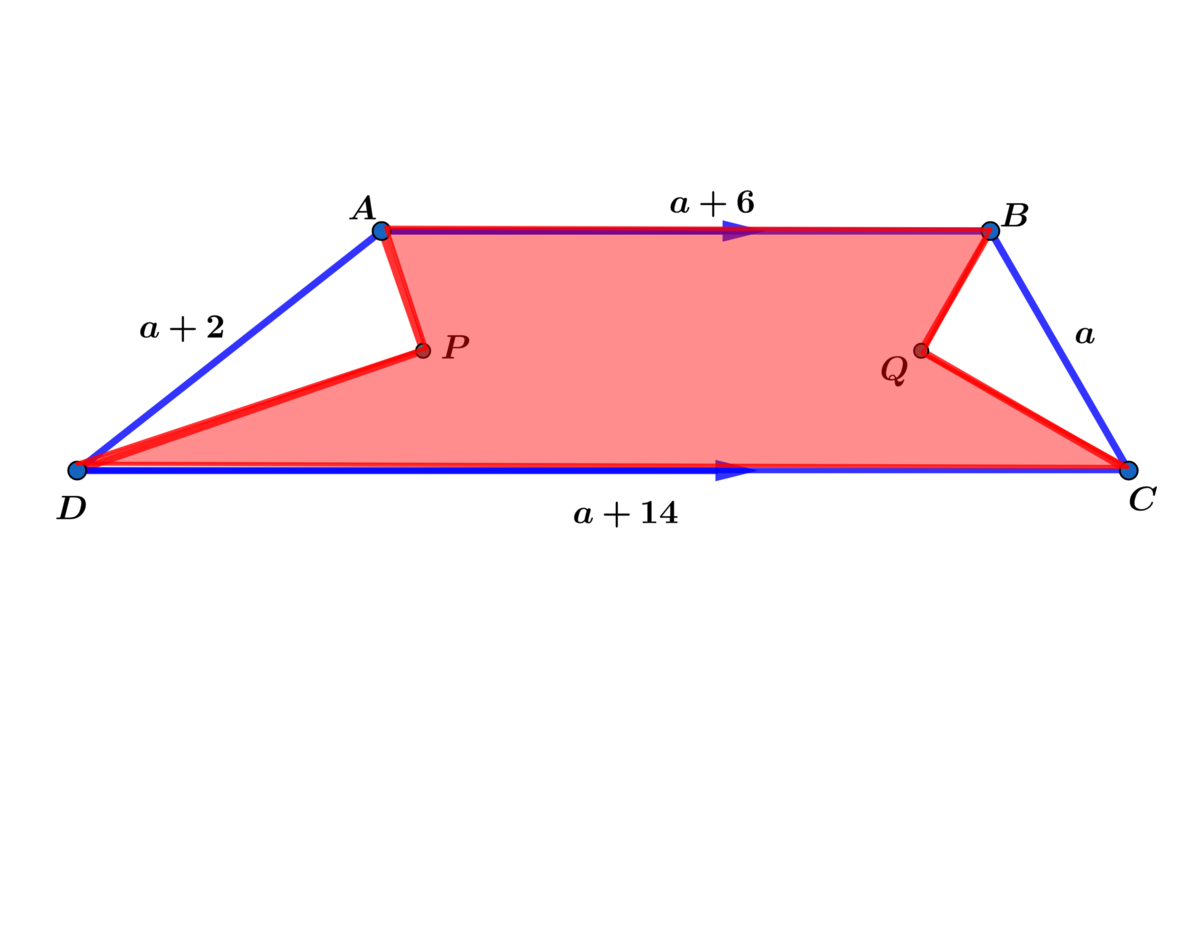
In Trapezoid A B C D , with A B ∥ C D and A B = a + 6 , D C = a + 1 4 , A D = a + 2 and B C = a , angle bisectors A P and D P intersect at P and angle bisectors B Q and C Q intersect at Q .
If the value of a for which the area of the hexagon A A B Q C D P = 8 a + 1 9 can be expressed as a = α − α + β , where α and β are coprime positive integers, find α + β .
The answer is 256.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Label the diagram as follows:
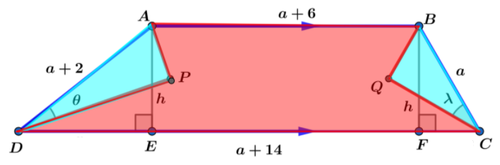
Since C Q is an angle bisector, ∠ B C F = 2 λ , and from right △ B C F , h = a sin 2 λ and F C = a 2 − h 2 . Similarly, on right △ A D E , h = ( a + 2 ) sin 2 θ and D E = ( a + 2 ) 2 − h 2 . D E + F C = D C − A B = ( a + 1 4 ) − ( a + 6 ) = 8 , so:
( a + 2 ) 2 − h 2 + a 2 − h 2 = 8
The area of trapezoid A B C D is A trap = 2 1 ( a + 6 + a + 1 4 ) h or A trap = ( a + 1 0 ) h .
Since A B ∣ ∣ D C , ∠ A B C = 1 8 0 ° − 2 λ , and since BQ is an angle bisector, ∠ C B Q = 9 0 ° − λ . Then by the angle sum of △ B Q C , ∠ B Q C = 9 0 ° . Therefore, B Q = a sin λ and C Q = a cos λ , so that the area of △ B Q C is T 1 = 2 1 ⋅ B Q ⋅ C Q = 2 1 ⋅ a sin λ ⋅ a cos λ = 4 1 a 2 ( 2 sin λ cos λ ) = 4 1 a 2 sin 2 λ which after substituting h = a sin 2 λ from above, T 1 = 4 1 a h .
By a similar argument, the area of △ A D E is T 2 = 4 1 ( a + 2 ) h .
The area of hexagon A B Q C D P is the area of the trapezoid minus the two right triangles, or A A B Q C D P = A trap − T 1 − T 2 = 8 1 ( a + 1 9 ) , so that:
( a + 1 0 ) h − 4 1 a h − 4 1 ( a + 2 ) h = 8 1 ( a + 1 9 )
The two equations solve to h = 4 1 and a = 1 5 − 1 5 + 2 4 1 for a > 0 .
Therefore, α = 1 5 , β = 2 4 1 , and α + β = 2 5 6 .
h 2 = ( a + 2 ) 2 − x 2 = a 2 − ( 8 − x ) 2 ⟹
a 2 + 4 a + 4 − x 2 = a 2 − 6 4 + 1 6 x − x 2 ⟹ a + 1 = 4 x − 1 6 ⟹
x = 4 a + 1 7 = D E ⟹ F E = 4 1 5 − a and h = 4 1 5 ( a + 5 ) ( a − 3 )
⟹ A T r a p e z o i d = 2 1 ( 2 ( a + 1 0 ) ) 4 1 5 ( a + 5 ) ( a − 3 ) = ( a + 1 0 ) 4 1 5 ( a + 5 ) ( a − 3 )
We want: A A B Q C D P = A T r a p e z o i d − ( A △ B Q C + A △ A P D )
A B ∥ D C ⟹ m ∠ B + m ∠ C = 1 8 0 ∘ and m ∠ A + m ∠ D = 1 8 0 ∘ ⟹
2 1 m ∠ B + 2 1 m ∠ C = 9 0 ∘ and 2 1 m ∠ A + 2 1 m ∠ D = 9 0 ∘
⟹ △ A P D and △ B Q C are right triangles ⟹ ∠ A P D = 9 0 ∘ and ∠ B Q C = 9 0 ∘
For △ B Q C :
cos ( 2 λ ) = 4 a 1 5 − a ⟹ cos ( λ ) = 2 1 + 4 a 1 5 − a = 8 a 3 ( a + 5 ) = 2 1 2 a 3 ( a + 5 )
⟹ sin ( λ ) = 2 1 2 a 5 ( a − 3 ) ⟹ B Q = 2 a 2 a 5 ( a − 3 ) and Q C = 2 a 2 a 3 ( a + 5 )
⟹ A △ B Q C = 1 6 1 5 ( a − 3 ) ( a + 5 ) a
For △ A P D :
cos ( 2 θ ) = 4 ( a + 2 ) a + 1 7 ⟹ cos ( θ ) = 2 1 + 4 ( a + 2 ) a + 1 7 = 8 ( a + 2 ) 5 ( a + 5 ) =
2 1 2 ( a + 2 ) 5 ( a + 5 )
⟹ sin ( θ ) = 2 1 2 ( a + 2 3 ( a − 3 ) ⟹ A P = 2 a + 2 2 ( a + 2 3 ( a − 3 )
and D P = 2 a + 2 2 ( a + 2 ) 5 ( a + 5 ) ⟹ A △ A P D = 1 6 1 5 ( a − 3 ) ( a + 5 ) ( a + 2 )
⟹ A A B Q C D P = A T r a p e z o i d − ( A △ B Q C + A △ A P D ) = 8 a + 1 9 1 5 ( a − 3 ) ( a + 5 )
= 8 a + 1 9 ⟹ 1 5 ( a 2 + 2 a − 1 5 ) = 1 ⟹ 1 5 a 2 + 3 0 a − 2 2 6 = 0
dropping the negative root ⟹ a = 1 5 − 1 5 + 3 6 1 5 = 1 5 − 1 5 + 1 5 2 4 1 =
1 5 1 5 ( − 1 5 + 2 4 1 ) = 1 5 − 1 5 + 2 4 1 =
α − α + β ⟹ α + β = 2 5 6 .