Trapped Circles
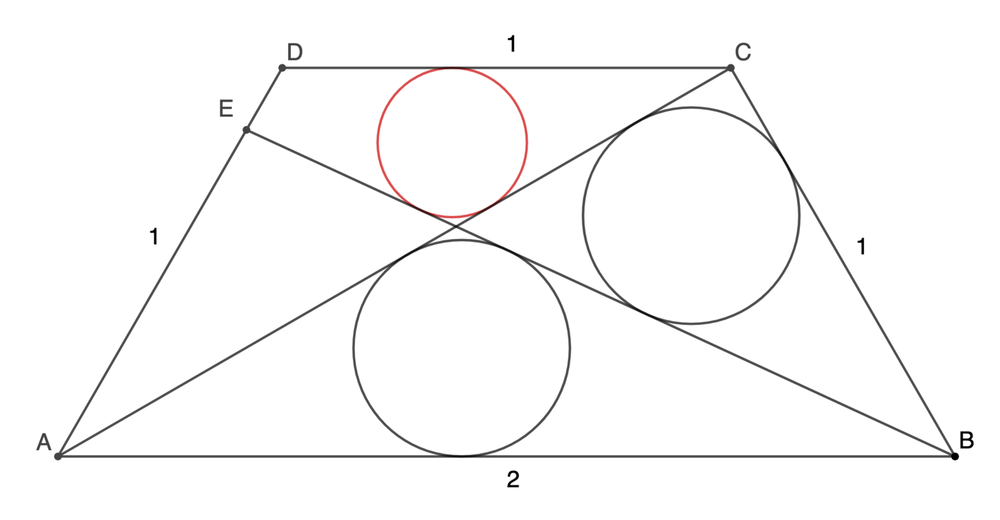
A B C D is an isosceles trapezoid with three equal sides. B C = C D = D A = 1 , A B = 2 . E is chosen so that the two black circles are congruent. If the radius of the red circle, r , is
r = c − a + b + a + b ,
submit a + b + c .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thank you for sharing the sangaku resources, Thanos. I love reading them.
Log in to reply
Thanks. I enjoy your return to the creative utilization of congruent incircles.
Let F be the intersection of B E and A C , and extend C D and B E to meet at G .
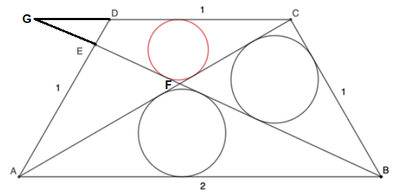
Since the trapezoid is a combination of three unit equilateral triangles, A C = 2 ⋅ 2 3 = 3 , and since A C 2 + B C 2 = A B 2 , by the converse of the Pythagorean Theorem ∠ A C B is a right triangle.
Let k = C F . Then A F = A C − C F = 3 − k , and by the Pythagorean Theorem, B F = C F 2 + B C 2 = k 2 + 1 .
The area of △ A F B is A △ A F B = 2 1 ⋅ A F ⋅ B C = 2 1 ⋅ ( 3 − k ) ⋅ 1 = 2 1 ( 3 − k ) , and the perimeter of △ A F B is P △ A F B = A F + B F + A B = 3 − k + k 2 + 1 + 2 .
The congruent inradii of △ B F C and △ A F B is R = 2 1 ( C F + B C − B F ) = P △ A F B 2 A △ A F B , or R = 2 1 ( k + 1 − k 2 + 1 ) = 3 − k + k 2 + 1 + 2 3 − k , which solves to k = 2 2 and R = 4 1 ( 2 + 2 − 6 ) .
By alternate interior angles of parallel segments C G and A B , ∠ G C A = ∠ F B A and ∠ C G B = ∠ A B G , so △ C F G ∼ △ A F B by AA similarity, which means R r = A F C F , or 4 1 ( 2 + 2 − 6 ) r = 3 − 2 2 2 2 , which solves to r = 1 0 − 2 + 3 + 2 + 3 .
Therefore, a = 2 , b = 3 , c = 1 0 , and a + b + c = 1 5 .
I did it this way, but when it comes to the "which solves to" part, I don't have any idea which equations are possible for hand calculation and which is better to let WA doing the dirty work (hard to input the equations especially a long one on a phone, I kept deleting nearly finish typed equations because the little X got in the way).
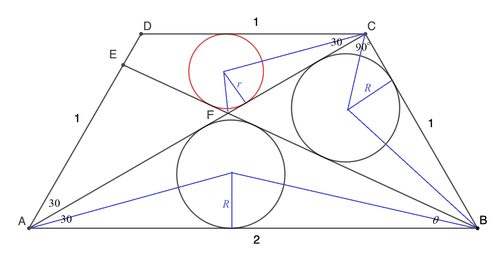
Let the radius of the black circles be R and that of the red circle be r , ∠ E B A = θ and A C and B E intersect at F .. Using the fact that the line joining the incircle and a vertex of the triangle bisects the vertex angle, we have:
R cot 2 ∠ C A B + R cot 2 ∠ E B A R cot 1 5 ∘ + R cot 2 θ R ( 2 + 3 ) + t R ⟹ R = A B = 2 = 2 = ( 2 + 3 ) t + 1 2 t Let t = tan 2 θ
Similarly,
R cot 2 ∠ C B E + R cot 2 ∠ A C B R cot ( 3 0 ∘ − 2 θ ) + R cot 4 5 ∘ R ( 1 − 3 t 3 + t ) + R ⟹ R = B C = 1 = 1 = 1 + 3 + ( 1 − 3 ) t 1 − 3 t
Therefore
( 2 + 3 ) t + 1 2 t 2 ( 1 + 3 ) t + 2 ( 1 − 3 ) t 2 5 t 2 + 2 3 t − 1 ⟹ t ⟹ tan θ = 1 + 3 + ( 1 − 3 ) t 1 − 3 t = 1 + 2 t − ( 2 3 + 3 ) t 2 = 0 = 5 2 2 − 3 − 1 − t 2 2 t = 4 2 − 3 3
Similarly for the red circle,
r cot 2 ∠ E F C + r cot 2 ∠ D C F r cot ( 7 5 ∘ − 2 θ ) + r cot 1 5 ∘ r ( 1 − ( 2 − 3 ) t 2 − 3 + t + 2 + 3 ) 1 − ( 2 − 3 ) t 4 r ⟹ r = F C = tan ( 6 0 ∘ − θ ) = 1 + 3 ( 4 2 − 3 3 ) 3 − 4 2 + 3 3 = 2 1 = 4 2 1 − ( 2 − 3 ) t = 2 0 2 5 − ( 2 − 3 ) ( 2 2 − 3 ) = 1 0 2 1 − 2 2 + 3 + 6 = 1 0 − 2 + 3 + 1 0 1 ⋅ 2 1 + 3 = 1 0 − 2 + 3 + 1 0 1 ( 2 1 + 3 ) 2 = 1 0 − 2 + 3 + 2 + 3
Therefore (a+b+c = 2+3+10 = \boxed {15}}.
In this solution we use the fact that, in the case where the two black incircles are congruent, the following relation holds: B F = s ⋅ ( s − b ) ( 1 ) where b = C A and s is the semiperimeter of △ A B C .
This is problem 2.2.5 in Fukagawa, Hidetoshi, and Dan Pedhoe. 1989, Japanese temple geometry problems, Winnipeg: Charles Babbage Research Centre. In this book no solution is given, but you can find one here (problem 8).
Reffering to the figure, let C H ⊥ A B . Let G be the intersection of lines C D and E B . Denote by r and R the radii of the red and black circles respectively.
Since H C = 2 A B − D C = 2 1 = 2 B C , we conclude that ∠ C B H = 6 0 ∘ .
By cosine rule on △ A B C ,
A C 2 = A B 2 + B C 2 − 2 A C ⋅ B C ⋅ cos B = 4 + 1 − 2 × 2 × 1 × 2 1 = 3 ⇒ A C = 3 This means that △ A B C is a right triangle, with ∠ C = 9 0 ∘ .
Using proposition ( 1 ) , we have B F 2 = s ( s − b ) = 2 2 + 1 + 3 ⋅ 2 2 + 1 − 3 = 2 3 ⇒ B F = 2 3 By Pythagorean Theorem on △ B C F ,
C F 2 = B F 2 − B C 2 = 2 3 − 1 = 2 1 ⇒ C F = 2 2 Furthermore, △ C G F ∼ △ A B F , thus,
F B G F = F A C F = A B G C ⇒ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ G F = F B ⋅ F A C F = 2 3 ⋅ 3 − 2 2 2 2 = 1 0 6 + 6 G C = A B ⋅ F A C F = 2 ⋅ 3 − 2 2 2 2 = 5 6 + 1 For the inradius of the right triangle B C F we have
R = s − B F = 2 1 ( B C + C F − B F ) = 2 1 ( 1 + 2 2 − 2 3 ) Again, due to the similarity of △ C G F and △ A B F ,
R r = A B G C ⇒ r = R ⋅ A B G C = 2 1 ( 1 + 2 2 − 2 3 ) ⋅ 2 5 6 + 1 = 1 0 1 ( − 2 + 3 + 2 + 3 ) For the answer, a = 2 , b = 3 , c = 1 0 , thus, a + b + c = 1 5 .