Trapped light
Optical fibers are devices used for guiding light in many applications, most notably for fast communication. A fiber consists of a glass cylinder surrounded by a wall covered in a special coating.
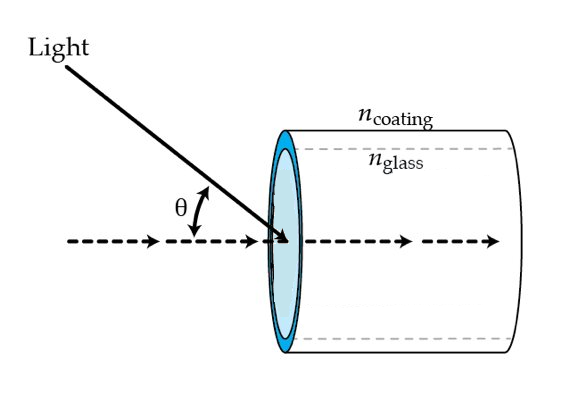
The fibers work on a principle called total internal reflection : light enters the fiber at an angle such that it does not get transmitted through the wall of the fiber when it hits the inside of the wall. Therefore, the refraction index of the glass part of the fiber has to be higher than that of its coating.
What is the maximum entering angle in degrees a light ray can pass from the air to the glass fiber for the total internal reflection to occur?
Details and Assumptions:
- Measure the entering angle from the axis of the fiber.
- Use the following refraction indexes: n air = 1 . 0 0 , n glass = 1 . 5 0 , and n coating = 1 . 4 6 .
The answer is 20.126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Nice solution. Could you explain the last step?
Call the angle of refraction from the air to the glass α . Then by Snell's Law we have:
n a i r sin θ = n g l a s s sin α
Call the angle of incidence from the glass to the coating β , and the angle of refraction from the glass to the coating γ . Then we have:
n g l a s s sin β = n c o a t i n g sin γ
In order for the light to be not be transmitted through the coating, we want γ = 9 0 ∘ . We also note that β = 9 0 ∘ − α , since the surface runs parallel to the axis. So we have:
n g l a s s sin ( 9 0 ∘ − α ) = n c o a t i n g sin 9 0 ∘
Substituting values, we solve for α = 1 3 . 2 6 1 5 ∘ .
Then we have:
n a i r sin θ = n g l a s s sin 1 3 . 2 6 1 5 ∘
θ = 2 0 . 1 2 6 4 ∘
Applying the law of refraction, we deduce that the angle of incidence of light passing from glass fiber to the coating must be larger than r l i m i t = a r c s i n n g n c = 7 6 . 7 3 8 5 ∘
→ i ≤ 9 0 ∘ − r l i m i t = 1 3 . 2 6 1 5 ∘ (i is the angle of refraction when light pass from air to glass)
→ θ ≤ a r c s i n ( n g sin i ) ⇒ θ ≤ 2 0 . 1 2 6 ∘
- theta: angle of incidence, alpha: angle of refraction between air and the glass that
---> sin(theta) = (n glass/n air)*sin(alpha)
- 90 deg - alpha: critical angle between the glass and the coating of the fiber
---> sin(90-alpha) = cos(alpha) = (n coating/n glass)
-
sin(alpha) = sqrt(1-(cos(alpha))^2)
-
theta = arcsin[(n glass/n air) sqrt(1-(n_coating/n_glass)^2)] = arcsin[(1.50) sqrt(1-(1.46/1.50)^2)] = arcsin(0.34409) = 20.126 deg
In order to a total reflexion the Snell's Law must be analysed: n1sina=n2sinb (. N1 and n2 are the refective index of the medias, and "a" and "b" the angles of incidence and refration). In that case, sin(b) must be higher or equal to 1. It is known that doesn't exist such an angle which sine>1, what really happens is that when the caculeted angle turns into 1, the light rays won't pass for the other media, occuring the total reflection. In the problem, the angle which the light makes with axis of the fiber at the glass is relatated with angle of incidence \alpha
The entering light refracts according to the law n a i r sin ( α ) = n g l a s s sin ( β ) .
When it hits the coating-glass boundary, it refracts according to the equation: n g l a s s cos ( β ) = n c o a t i n g sin ( 2 π ) = n c o a t i n g .
Therefore, the entering angle should be sin ( α ) = n a i r n g l a s s × 1 − ( n a i r n c o a t i n g ) 2 .
Solving for α we get 2 0 . 1 2 6 ∘ .
We have critical angle of this problem
sin θ c = cos θ 1 = n 1 n 2 . . . . ( 1 ) ,
Use snell laws we get:
n a i r ⋅ sin θ = n 1 ⋅ sin θ 1 ,
sin θ 1 = n 1 sin θ . . . . ( 2 ) ,
Use (...1) and (...2), we get: ( n 1 n 2 ) 2 + ( n 1 sin θ ) 2 = 1 , θ = arcsin n 1 2 − n 2 2 = arcsin 1 . 5 0 2 − 1 . 4 6 2 = 2 0 . 1 3 ∘
A figure to substantiate the solution would have been nice. But bear with it.
Let us consider the time when the light ray has entered the cylinder and is incident on the glass-coating interface. The angle of incidence is α . So, n g l a s s ⋅ sin α = n c o a t i n g ⋅ sin 9 0 ∘
Thus the angle of refraction in air-glass interface is 9 0 ∘ − α .
So, θ and α are related by,
n g l a s s ⋅ cos α = n a i r ⋅ sin θ
which gives sin θ = ( n g l a s s 2 − n c o a t i n g 2 ) , i.e. θ is around 20.12.