Travel inside Square
Square with side length 6 with A = ( 0 , 0 ) , B = ( 6 , 0 ) , C = ( 6 , 6 ) , D = ( 0 , 6 ) . Points P ( 1 , 3 ) , Q ( 5 , 1 ) are inside the square. You want to travel from point P to point Q off the all sides of the square (one side - one visit while traveling). Find the shortest possible path from P to Q under these conditions. The shortest path length can be expressed as d = c .
As your answer, enter c .
The answer is 164.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks for attention. Fine solution. Happy New Year!!!
Wow, that's really an amazing solution! It would've never come to my mind! Congrats, @David Vreken
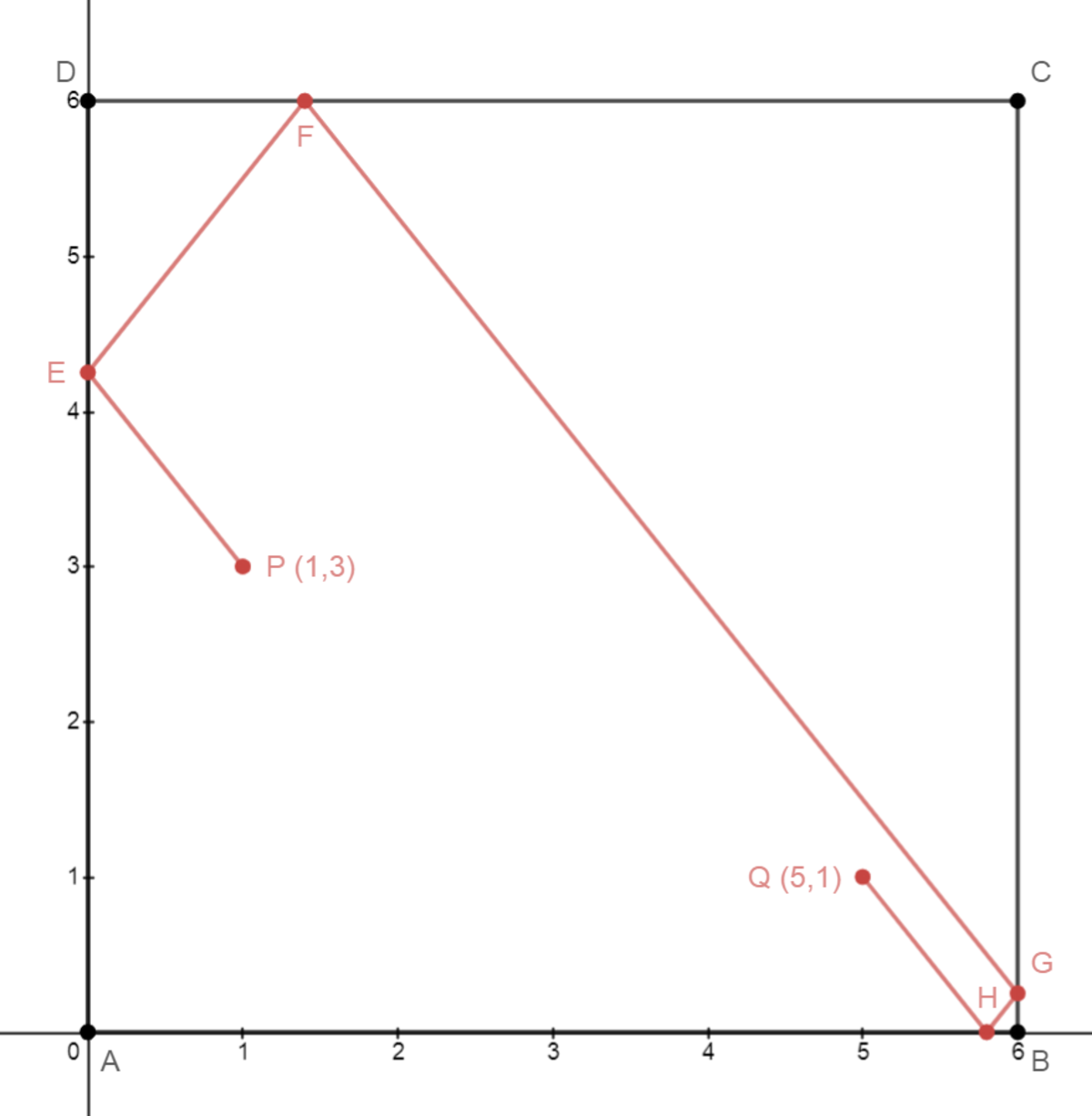
The shortest path travelled from two points is one travelled by light. The shortest distance travelled from P and Q is one travelled by light where the four internal sides of the square serve as mirrors. Then the path from P to the final image of Q is a straight line. Let us consider the x -component and y -component of the absolute distance travelled (disregard the direction) by the beam of light.
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ∣ x P Q ∣ = 1 ∣ x P E ∣ + 6 ∣ x E F ∣ + ∣ x F G ∣ + 1 ∣ x G H ∣ + ∣ x H Q ∣ = 8 ∣ y P Q ∣ = 3 ∣ y P F ∣ + ∣ y E F ∣ + 6 ∣ y F G ∣ + ∣ y G H ∣ + 1 ∣ y H Q ∣ = 1 0
Then the shortest path between P and Q s = ∣ x P Q ∣ 2 + ∣ y P Q ∣ 2 = 1 6 4 . Therefore c = 1 6 4 .
Thanks for attention. Fine solution. Happy New Year!!!
Reflect the square and Q several times as follows:
In order to meet the condition of one visit per side while traveling, the segment must pass through two horizontal square segments and two vertical square segments, and there are four possibilities as shown above: P Q ′ , P Q ′ ′ , P Q ′ ′ ′ , and P Q ′ ′ ′ ′ .
Using the fact that each square has a side length of 6 and each Q is 1 unit vertically and 1 unit horizontally away from the side of those squares, the coordinates of each reflected Q are:
Q ′ ( − 6 − 1 , 2 ⋅ 6 + 1 ) = Q ′ ( − 7 , 1 3 )
Q ′ ′ ( 3 ⋅ 6 − 1 , 2 ⋅ 6 + 1 ) = Q ′ ′ ( 1 7 , 1 3 )
Q ′ ′ ′ ( − 6 − 1 , − 2 ⋅ 6 + 1 ) = Q ′ ′ ′ ( − 7 , − 1 1 )
Q ′ ′ ′ ′ ( 3 ⋅ 6 − 1 , − 2 ⋅ 6 + 1 ) = Q ′ ′ ′ ( 1 7 , − 1 1 )
And each P Q option has a length of:
P Q ′ = ( 1 − − 7 ) 2 + ( 3 − 1 3 ) 2 = 1 6 4
P Q ′ ′ = ( 1 − 1 7 ) 2 + ( 3 − 1 3 ) 2 = 3 5 6
P Q ′ ′ ′ = ( 1 − − 7 ) 2 + ( 3 − − 1 1 ) 2 = 2 6 0
P Q ′ ′ ′ ′ = ( 1 − 1 7 ) 2 + ( 3 − − 1 1 ) 2 = 4 5 2
The shortest possible path is P Q ′ = 1 6 4 , so c = 1 6 4 .