Traveling Through Triangles
Brilli the ant stands on node 1 of the figure below.
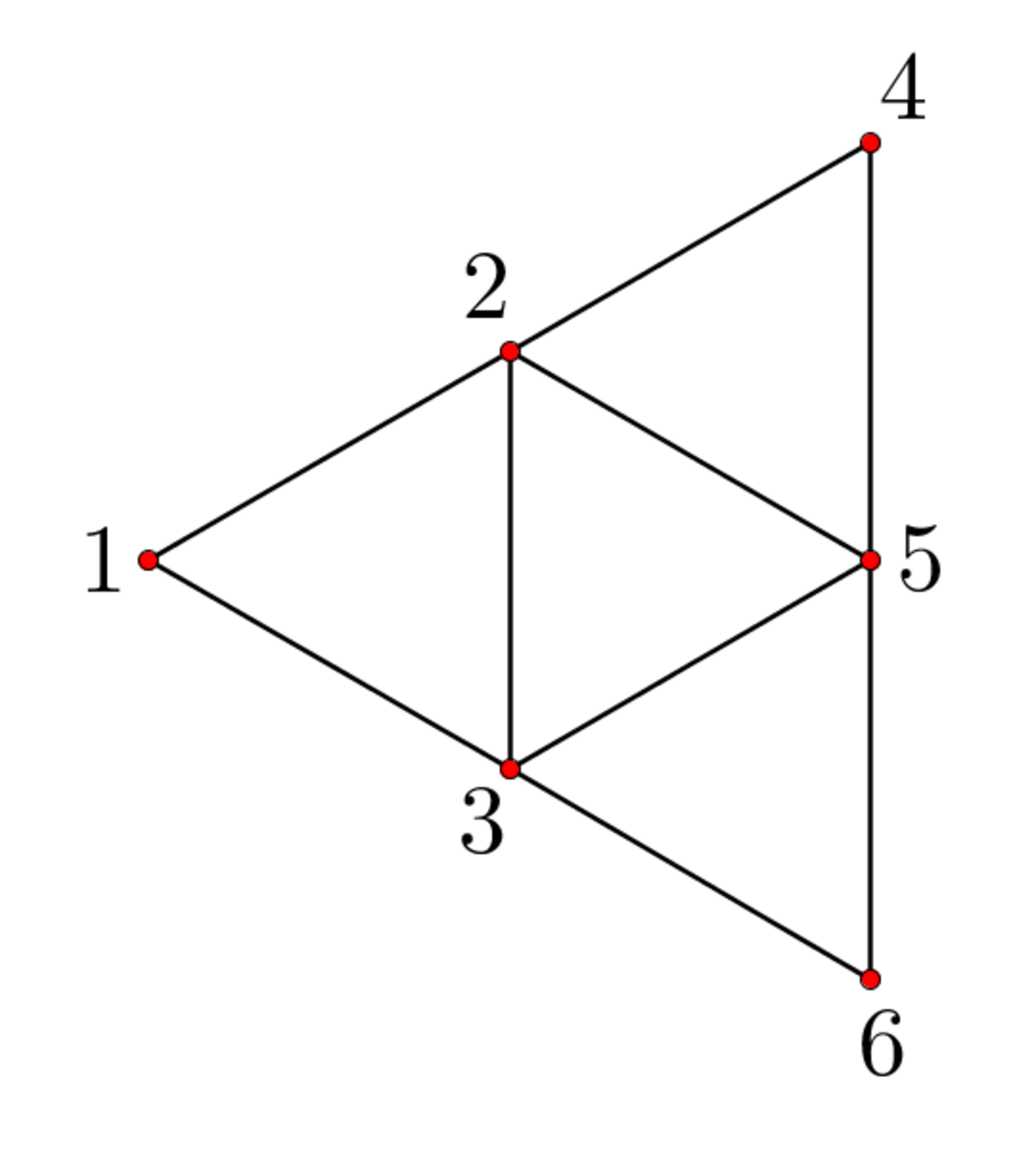
Every minute, Brilli picks an adjacent node at random and moves to it. Each adjacent node has the same chance to be picked. For example, when Brilli is on node 2, he could move to nodes 1, 3, 4, or 5, each with a probability.
What is the expected value of the number of moves Brilli will need to make to get to node 5?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Expected Value - Problem Solving
Let X m → n be a random variable that represents the number of moves to get from node m to node n .
The goal is to find E [ X 1 → 5 ] .
Due to the symmetry in the problem, it can be assumed that E [ X 2 → 5 ] = E [ X 3 → 5 ] and E [ X 4 → 5 ] = E [ X 6 → 5 ]
Let a = E [ X 1 → 5 ] , b = E [ X 2 → 5 ] , and c = E [ X 4 → 5 ] .
Using linearity of expectation and the identities above, the following system of equations can be written:
a = b + 1
b = 4 1 a + 4 1 b + 4 1 c + 1
c = 2 1 b + 1
Solving this system of equations yields a = 5 .
Therefore, the expected number of moves required to get to node 5 is 5 .