Traversing Circles
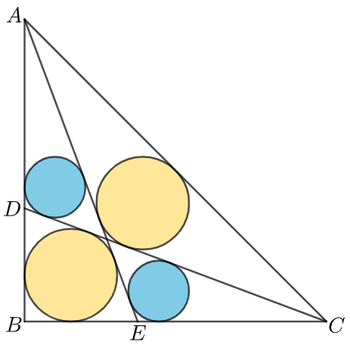
In the isosceles right triangle △ A B C with two legs both of a unit length, points D and E are selected, such that A E and D C form two congruent orange circles and two congruent blue circles.
If the radius of the blue circle is r , input ⌊ 1 0 6 r ⌋ as your answer.
The answer is 100644.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
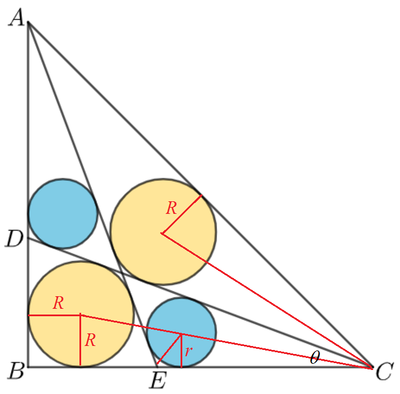
Let the radius of the orange circle be R and ∠ D C B = θ . From the lower orange circle, we have:
R + R cot 2 θ R + t R ⟹ R = B E = 1 = 1 = 1 + t t Let t = tan 2 θ
From the upper orange circle,
2 1 A C R ⟹ 2 R = tan ( 2 4 5 ∘ − θ ) = 1 + ( 2 − 1 ) t 2 − 1 − t Note that tan 2 2 . 5 ∘ = 2 − 1
Therefore we have:
1 + t 2 t ⟹ t = 1 + ( 2 − 1 ) t 2 − 1 − t = 3 − 2 2 2 − 1 − 1
Now consider the lower blue circle,
r cot 2 ∠ A E C + r cot 2 ∠ D C B r cot ( 2 9 0 ∘ + θ ) + r cot 2 θ r ( 1 + t 1 − t + t 1 ) t ( 1 + t ) 1 + 2 t − t 2 ⋅ r ⟹ r ⟹ ⌊ 1 0 6 r ⌋ = C E = 1 − tan θ = 1 − 1 − t 2 2 t = 1 − t 2 1 − 2 t − t 2 = ( 1 − t ) ( 1 + 2 t − t 2 ) t ( 1 − 2 t − t 2 ) = 9 9 1 2 − 7 0 2 8 2 + 3 7 5 8 2 − 1 − 2 6 2 0 2 ( 2 − 1 ) 1 3 7 1 − 9 7 5 2 + 4 1 6 4 2 − 1 − 2 9 3 5 2 ( 2 − 1 ) ≈ 0 . 1 0 0 6 4 4 3 7 5 = 1 0 0 6 4 4
Place the whole diagram on a coordinate plane so that B is at the origin, A is at A ( 0 , 1 ) , and C is at C ( 1 , 0 ) , and let F be the intersection of A E and D C at F ( k , k ) . Also, let M be the midpoint of A C at M ( 2 1 , 2 1 ) .
Then A F has the equation y = k k − 1 x + 1 and an x -intercept of E ( 1 − k k , 0 ) .
By the distance equation, A E = 1 + ( 1 − k ) 2 k 2 , A F = F C = k 2 + ( k − 1 ) 2 , D F = F E = k 2 + ( k − 1 − k k ) 2 , F M = ( 2 1 − k ) 2 , and A C = 2 .
The inradius of right △ A B E is R = 2 1 ( A B + B E − A E ) = 2 1 ( 1 + 1 − k k − 1 + ( 1 − k ) 2 k 2 ) .
The inradius of △ A F C is R = P △ A F C 2 A △ A F C = A F + F C + A C 2 ⋅ 2 1 ⋅ A C ⋅ F M = 2 k 2 + ( k − 1 ) 2 + 2 2 ⋅ ( 2 1 − k ) 2
Therefore, R = 2 1 ( 1 + 1 − k k − 1 + ( 1 − k ) 2 k 2 ) = 2 k 2 + ( k − 1 ) 2 + 2 2 ⋅ ( 2 1 − k ) 2 , which solves to k = 4 1 ( 2 − 2 ( 2 − 1 ) ) .
The inradius of △ F E C is r = P △ F E C 2 A △ F E C = E C + F E + F C 2 ⋅ 2 1 ⋅ E C ⋅ k = ( 1 − 1 − k k ) + k 2 + ( k − 1 − k k ) 2 + k 2 + ( k − 1 ) 2 ( 1 − 1 − k k ) ⋅ k , which after substituting k = 4 1 ( 2 − 2 ( 2 − 1 ) ) solves to r ≈ 0 . 1 0 0 6 4 4 , so ⌊ 1 0 6 r ⌋ = 1 0 0 6 4 4 .