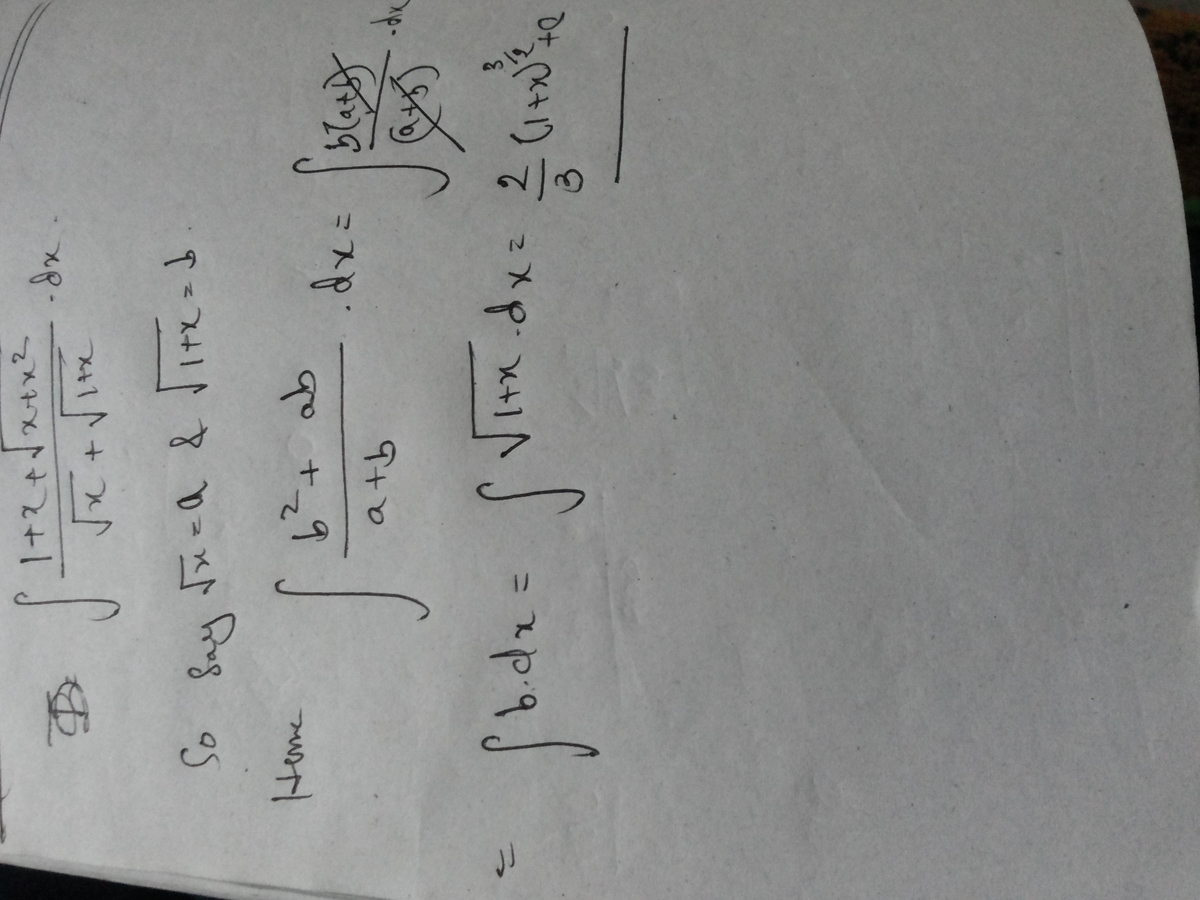A calculus problem by Achal Jain

Calculus Level 2

Find an indefinite integral to $\color{#D61F06} \displaystyle \int { \frac { 1+x+\sqrt { x+{ x }^{ 2 } } }{ \sqrt { x } +\sqrt { 1+x } } } \, dx$ .

Clarification: $C$ denotes the arbitrary constant of integration .

2(1+x)^{\dfrac{3}{2}} +C

\frac { 2{ (1+x) }^{ \dfrac { 3 }{ 2 } } }{ 3 } +C

\frac { 1\sqrt { 1+x } }{ 2 } +C

\sqrt{1+x} +C

1 solution

Md Zuhair
Feb 27, 2017

Pretty simple... we can do it like this...

That's why the title. instead of substitution i just took the x common part outside the bracket from the numerator which lead to cancellation of denominator.

Achal Jain - 4 years, 3 months ago

Ya sure it is always correct. But ibtaje a and b to make it easier

Md Zuhair - 4 years, 3 months ago

I did it by rationalising the polynomial.Your method is a much more simpler one.

Satwik Murarka - 4 years, 3 months ago

A calculus problem by Achal Jain

1 solution

0 pending reports