Triangle.
A B C is an isosceles triangle with A C = B C . Furthermore, D is a point on B C that bisects the angle at A .
If ∠ B = 7 2 ∘ and C D = 1 , then find length of B D (upto 3 decimal places).
The answer is 0.618.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Use of solution without trig functions
Golden ratio fascinating term. Thanks for the information
No need for golden ratio. Use Angle bisector theorem
We observe that ∠ A D B = 7 2 and 1 = ∣ A D ∣ = ∣ A B ∣ .
Let ∣ B D ∣ = x
Therefore:
1 1 + x = x 1
⟹ x 2 + x − 1 = 0
Solving the quadratic yields:
x 1 = 2 − 1 + 5
x 2 = 2 − 1 − 5
The side can only take the positive value which is
ϕ − 1 ≈ 0 . 6 1 8
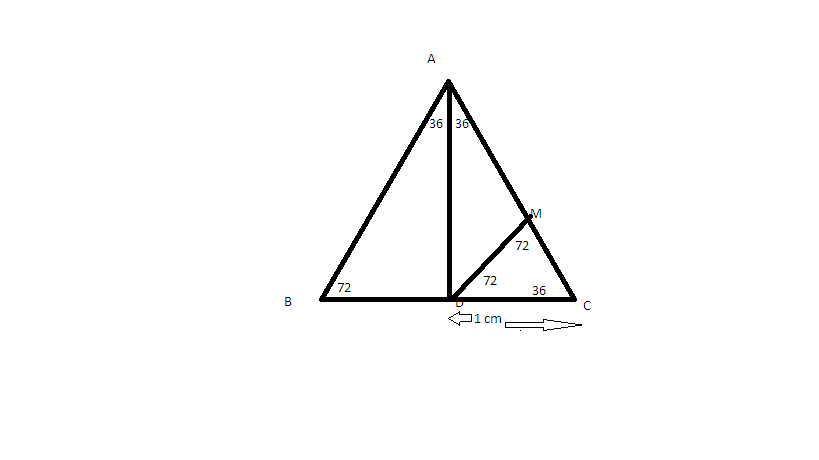 Triangle CMD ~Triangle CAD
CM/CA=MD/AB=1/CB
1/CA=MD/AB=1/1+ BD
1+BD=CA
By using cos rule ,
cos 36=(CD^2 + AC^2 - AD^2)/2.CD.AC=(5^1/2 + 1)/2
BD=(5^1/2 - 1)/2
BD~0.618
Triangle CMD ~Triangle CAD
CM/CA=MD/AB=1/CB
1/CA=MD/AB=1/1+ BD
1+BD=CA
By using cos rule ,
cos 36=(CD^2 + AC^2 - AD^2)/2.CD.AC=(5^1/2 + 1)/2
BD=(5^1/2 - 1)/2
BD~0.618
Hmm.. nice and constructive process, and can be easily done by sine rule.
Chasing down the angles, we see that triangle ACD is isoceles, and AD = CD =1. Applying the law of sines, AD/sin(72) = BD/sin(36), so BD = sin(36)/sin(72) = 0.618.
By the theorem of angle bisector A B : A C = C D : B D and A B = 2 A C × c o s α substituting that we get B D = 0 . 6 1 8
If the triangle is isosceles, each pink angle is 36º, and C is also 36º. Therefore, AD = 1. s e n 7 2 º 1 = s e n 3 6 ? --> ? = 0.6180339887 ~ 0.618
Angle B is 72. so 1/2 angle A is 36, and angle C is 36. Triangle ACD is isosceles; since CD = 1, AD =1. Triangle ADB is also isosceles, and AB = 1.Let DB = d; then by the Law of Cosines in triangle ADB, we have d^2 = 1^2+ 1^2 - 2(1)(1) cos(36), d = .618. Ed Gray
Golden Ratio Triangle
|AB| =1 , |AD| =1 , |DB| =x , |CA| =1+x
if its a 72,72,36 triangle there is "Golden Ratio" so 1+x=1.618 .... x=0.618