Origami?
Probability
Level
2
How many triangles are there in the figure below?
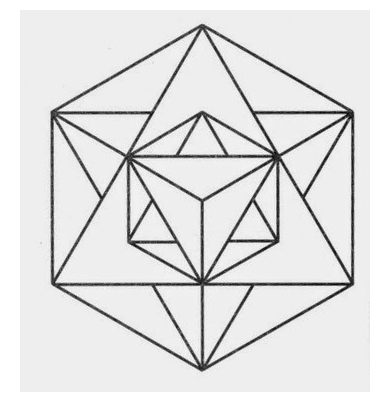
34
78
112
7!
56
100
Not more than 20
6!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Nice problem. :) There are 56 triangles total.
Ashish posted a clear breakdown of where they are in 4 categories. However, here is an exhaustive proof that no additional triangles exist. Ashish, your method of counting is certainly faster. However, the technique I used is cool in that it will work for any triangle counting problem.
Step 1 : Identify each vertex and, for convenience, group them into equivalent classes by symmetry.
Step 2 : For each vertex, consider every possible pair of lines extending out from it. Again, group for symmetry.
Step 3 : For each pair of lines extending from a vertex, a triangle exists if and only if a point on one line is connected by a line in the diagram, directly to a point on the other line. Counting these identifies every triangle that the selected vertex is part of.
Step 4 : Add up all of the triangles counted by this method and, finally, divide this sum by three because each has been triple counted (once for each vertex.)