Triangle Area Sum 2
Find all possible areas of a triangle with sides of lengths and and one angle.
If the sum of the areas of the smallest triangles is where and are integers and is square-free, enter your answer as .
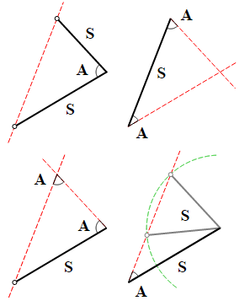
- This is part of the set Trevor's Ten .
- Useful Brilliant wiki: Area of a Triangle
- Image Credit: Wikimedia Congruent Triangles by Ilmari Karonen
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Through this solution, I will refer to law of cosines a 2 = b 2 + c 2 − 2 b c cos ( A ) as LOC and area of a triangle in terms of sine 2 1 a b sin C as ATS. Also, lower case letters represent sides while uppercase letters represent angles.
Begin with the simple case of a = 1 1 , b = 1 2 C = 6 0 .
ATS ⟹ 2 1 ( 1 1 ) ( 1 2 ) ( 2 3 ) = 3 3 3 ≈ 5 7 . 1 5 7
Now if a = 1 1 , b = 1 2 , A = 6 0
LOC ⟶ a 2 1 2 1 0 c ATS = b 2 + c 2 − 2 b c cos ( A ) = 1 4 4 + c 2 − 1 2 c = c 2 − 1 2 c + 2 3 = 6 ± 1 3 ⟹ 2 1 ( 6 ± 1 3 ) ( 1 2 ) ( 2 3 ) = 1 8 3 ± 3 3 9 ≈ 4 9 . 9 , 1 2 . 4
Now if a = 1 1 , b = 1 2 , B = 6 0
LOC ⟶ b 2 1 4 4 0 c ATS = a 2 + c 2 − 2 a c cos ( B ) = 1 2 1 + c 2 − 1 1 c = c 2 − 1 1 c − 2 3 = 2 1 1 ± 2 1 3 c can’t be negative, so ignore the - case ⟹ 2 1 ( 2 1 1 + 2 1 3 ) ( 1 1 ) ( 2 3 ) = something ugly we don’t care about ≈ 6 0 . 9 6
We have areas 6 0 . 9 6 > 5 7 . 2 > 4 9 . 9 > 1 2 . 4
Thus summing the three smallest we get ( 3 3 3 ) + ( 1 8 3 + 3 3 9 ) + ( 1 8 3 − 3 3 9 ) = 6 9 3
Therefore a b
a + b = 6 9 + 3 = 7 2