Triangle Bonanza.
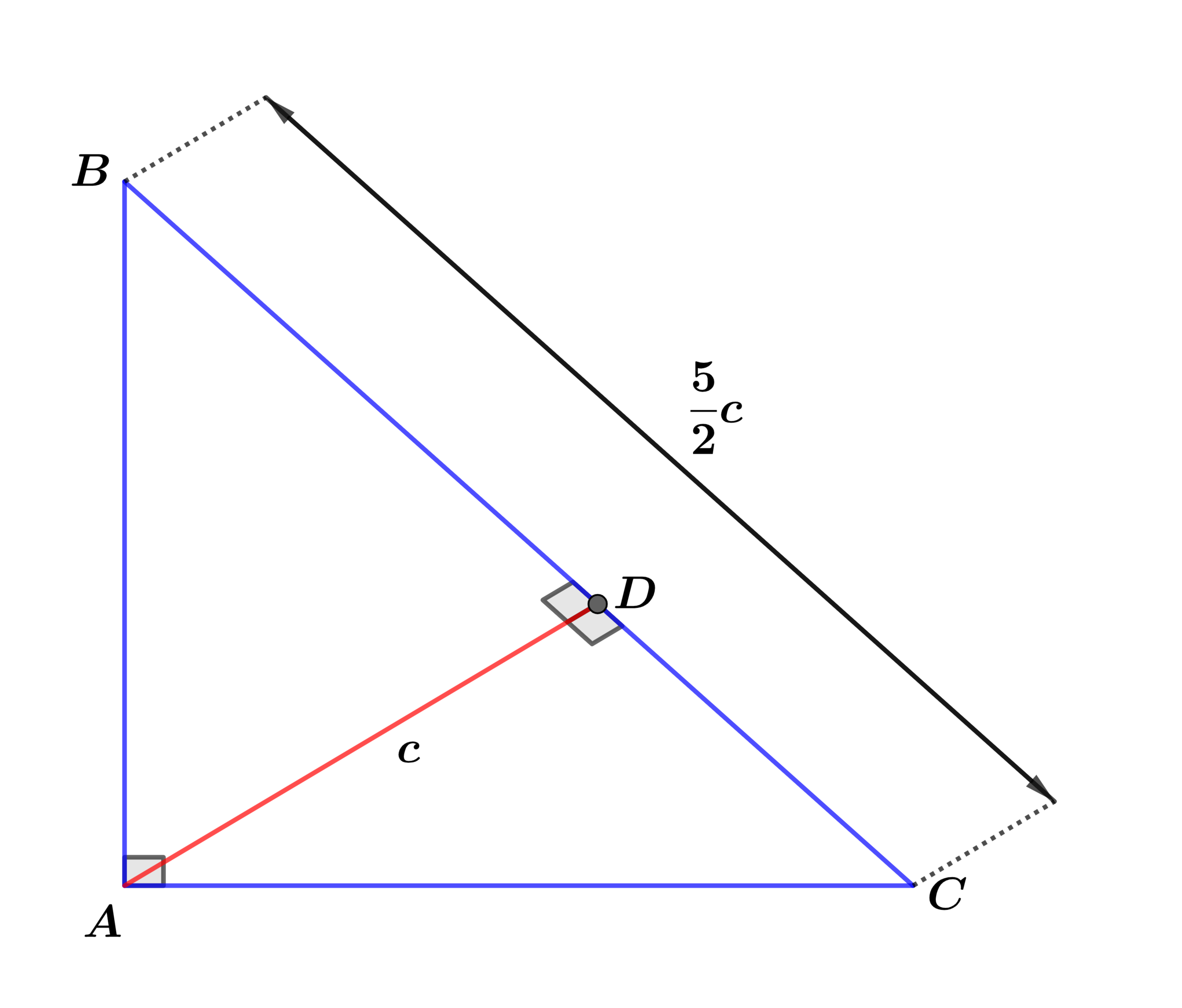
In right , is the altitude to hypotenuse with and .
If in right the perimeter and the value of can be expressed as
, where and are coprime positive integers, find .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For convenience let j = 2 5 (This is how I constructed the problem).
Note: j > = 2 ensures that △ A B C is a right triangle.
In △ A B C the altitude is the mean proportion between the segments of the hypotenuse
⟹ c 2 = x ( j c − x ) = ( j c ) x − x 2 ⟹ x 2 − ( j c ) x + c 2 = 0 ⟹
x = ( 2 j ± j 2 − 4 ) c
Using x = ( 2 j ± j 2 − 4 ) c ⟹ ∣ D C ∣ = ( 2 j − j 2 − 4 ) c and ∣ B D ∣ = ( 2 j + j 2 − 4 ) c
⟹ ∣ A C ∣ = ∣ A D ∣ 2 + ∣ D C ∣ 2 = 2 j 2 − j j 2 − 4 c
and
∣ A B ∣ = ∣ B D ∣ 2 + ∣ A D ∣ 2 = 2 j 2 + j j 2 − 4 c
Note: Using x = ( 2 j − j 2 − 4 ) c the values of ∣ A B ∣ and ∣ A C ∣ are just switched, so that ∣ A C ∣ = 2 j 2 + j j 2 − 4 and ∣ A B ∣ = 2 j 2 − j j 2 − 4 c .
Using j = 2 5 The Perimeter P = ( 2 3 5 + 5 ) c = c 2 ⟹
c ( c − ( 2 3 5 + 5 ) ) = 0 and c = 0 ⟹ c = 2 3 5 + 5 =
f d ∗ e + e ⟹ d + e + f = 1 0 .