Triangle Bound

Probability Level 5

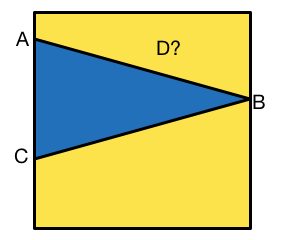In a unit square, points A, B, C are chosen uniformly at random on the perimeter, and point D is chosen uniformly at random in the unit square. To 4 decimal places, what is the probability that the D lies within triangle $ABC$ ?

Note: The probability is between 0 and 1.

Inspiration

The answer is 0.1563.

1 solution

Rajarshi Tiwari
Aug 5, 2015

!FORTRAN 90 PROGRAM FOR MONTE CARLO PROGRAM MAIN IMPLICIT NONE REAL(16) :: A(2),B(2),C(2),D(2) REAL(16) :: R0,R1,R2,R3 REAL(16) :: PROB, PREV INTEGER :: I, NUM,CIN,COUT

!NUM = 100000
CIN = 0 COUT = 0 I = 1 PROB = 0.0Q0 PREV = 0.0Q0 !DO I = 1, NUM
DO CALL GENERATE POINT ON PERIMETER(A) CALL GENERATE POINT ON PERIMETER(B) CALL GENERATE POINT ON PERIMETER(C) CALL RANDOM NUMBER(D)

 R0 = AREA_TRIANGLE(A,B,C)
 R1 = AREA_TRIANGLE(A,B,D)
 R2 = AREA_TRIANGLE(A,D,C)
 R3 = AREA_TRIANGLE(D,B,C)

 !PRINT*,R0,R1+R2+R3,R0-(R1+R2+R3)                                                                                                                                                                                                                                                                                        
 IF (ABS(R0-(R1+R2+R3)) <= 1.0E-30_16) THEN
    CIN = CIN + 1
 ELSE
    COUT = COUT + 1
 END IF
 PROB = DBLE(CIN)/DBLE(I)
 WRITE(*,'(2(F40.30,1X))'),PROB,PROB-PREV
 PREV = PROB
 !PAUSE                                                                                                                                                                                                                                                                                                                   
 !WRITE(*,*)DBLE(CIN)/DBLE(I), DBLE(COUT)/DBLE(I)                                                                                                                                                                                                                                                                         
 I = I + 1

END DO

CONTAINS

SUBROUTINE GENERATE POINT ON PERIMETER(PP) IMPLICIT NONE REAL(16), DIMENSION(:) :: PP REAL(16) :: X CALL RANDOM NUMBER(X)

X = X*4.0Q0

IF (X < 1.0Q0) THEN
   PP = [X,0.0Q0]
ELSE IF (X < 2.0Q0) THEN
   PP = [1.0Q0,X-1.0Q0]
ELSE IF (X < 3.0Q0) THEN
   PP = [3.0Q0-X,1.0Q0]
ELSE
   PP = [0.0Q0,4.0Q0-X]
END IF
RETURN

END SUBROUTINE GENERATE POINT ON_PERIMETER

FUNCTION AREA_TRIANGLE(X,Y,Z) RESULT(AR) IMPLICIT NONE REAL(16), DIMENSION(:) :: X,Y,Z REAL(16) :: AR

AR = X(1)*(Y(2)-Z(2)) + Y(1)*(Z(2)-X(2)) + Z(1)*(X(2)-Y(2))
AR = 0.5Q0 * AR
AR = ABS(AR)
RETURN

END FUNCTION AREA_TRIANGLE

END PROGRAM MAIN

I got this question wrong so I cannot submit a solution but seeing the right answer, I found my error, here is my non-comp sci solution:

The probability D is in the triangle is equivalent to the expected area of the triangle as the area of the square is $1$ .

We will find the expected area of the triangle with a weighted average of $4$ cases.

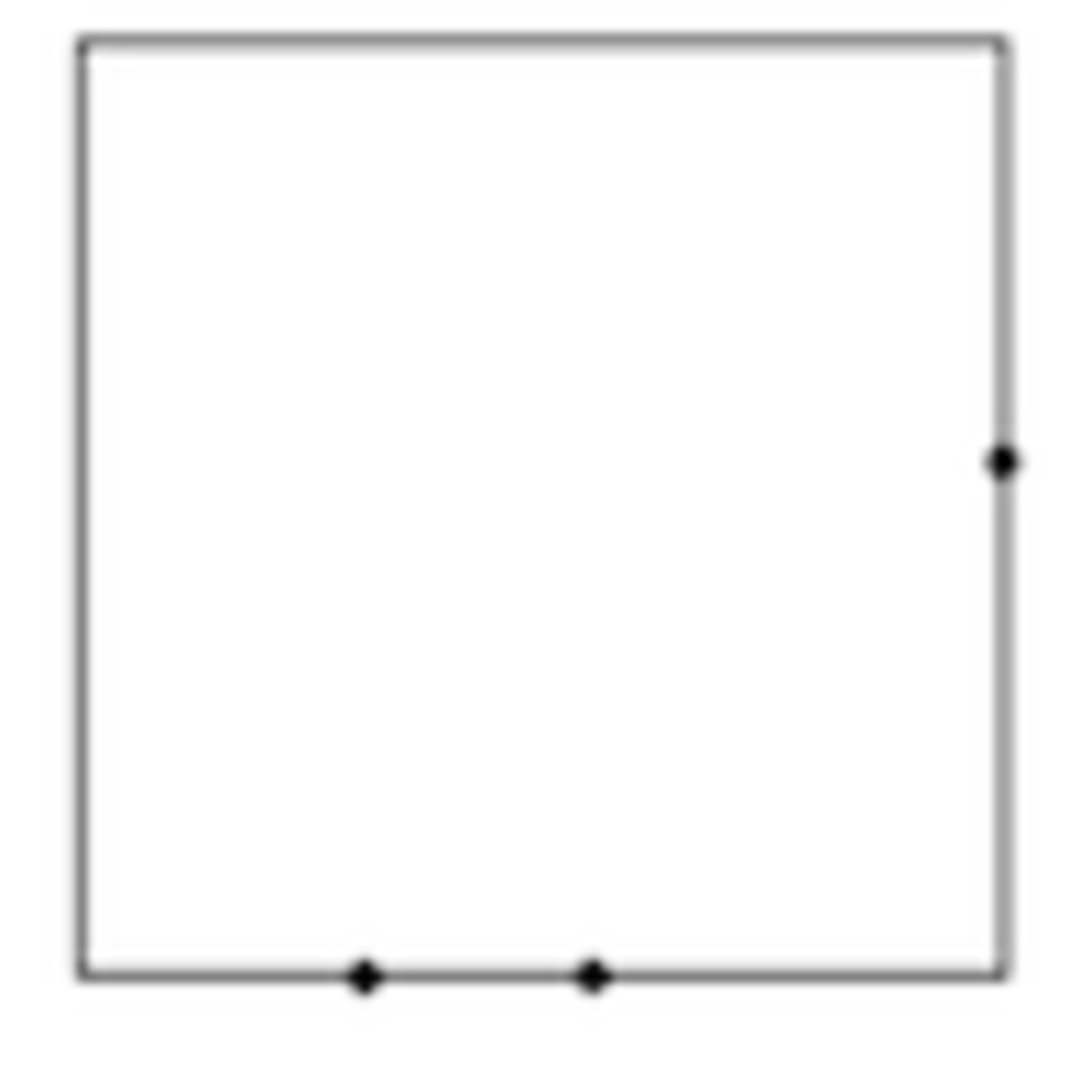
Fixing one point on the bottom of the triangle WLOG there is a $\frac{1}{16}$ chance all $3$ points will be on the same side, $\frac{^{3}P_{2}}{16}=\frac{3}{8}$ chance that all $3$ points will be on different sides, $\frac{^{3}P_{2}}{16}=\frac{3}{8}$ chance that two points will be on a side together and the third on an adjacent side, and then the remaining $\frac{3}{16}$ have two points on the same side and the third on the opposite side as depicted below:

Now we must find the average area of each one:

Case $1$ : all $3$ points are on one side

This case is trivial, the area is $0$

Case $2$ : all $3$ points on different sides

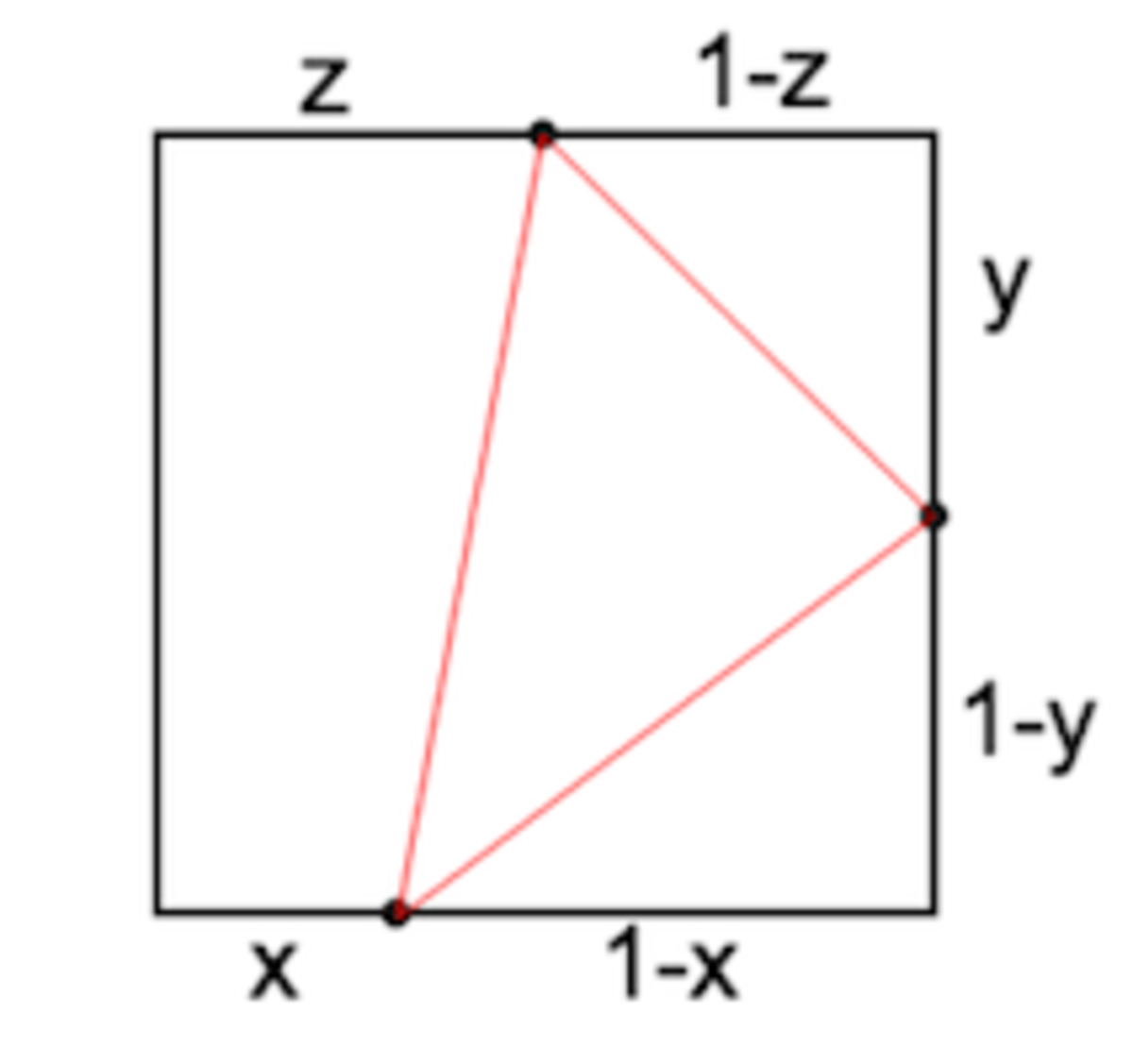
Now the area is $1-\frac{x+z}{2}-\frac{(1-x)(1-y)}{2}-\frac{y(1-z)}{2}$ given that the average values of $x$ , $y$ , and $z$ are all $\frac{1}{2}$ , the average value of this expression is $\frac{1}{4}$

Case $3$ : two points on one side and the third on an adjacent side

The three sub-segments of this diagram are exchangeable and thus have the same average length. As their sum is always $1$ that means each must have an average length $\frac{1}{3}$ , so the distance between two points on the same side averages $\frac{1}{3}$ . This is important for this case and the next.

The average length of the base (on the side with two points) is $\frac{1}{3}$ and the average height is $\frac{1}{2}$ thus the average area is $\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{3}=\frac{1}{12}$

Case $4$ : two points on one side and the third on the opposite side

The average length of the base (on the side with two points) is $\frac{1}{3}$ and the height is $1$ thus the average area is $\frac{1}{2}\cdot\frac{1}{3}\cdot1=\frac{1}{6}$

With a weighted average of the probability of a case occuring and the average area it yields we find the average area of any triangle and subsequently the probability to be $\frac{1}{16}\cdot0+\frac{3}{8}\cdot\frac{1}{4}+\frac{3}{8}\cdot\frac{1}{12}+\frac{3}{16}\cdot\frac{1}{6}=\boxed{\frac{5}{32}}$

Sean Sullivan - 5 years, 10 months ago

Nice Sean!

I must say, yours is a cooler solution, for being analytic.

Rajarshi Tiwari - 5 years, 10 months ago

Same story here, got fooled by the diagram.

Samrat Mukhopadhyay - 4 years, 8 months ago

Triangle Bound

The answer is 0.1563.

1 solution

0 pending reports