Triangle Cascade
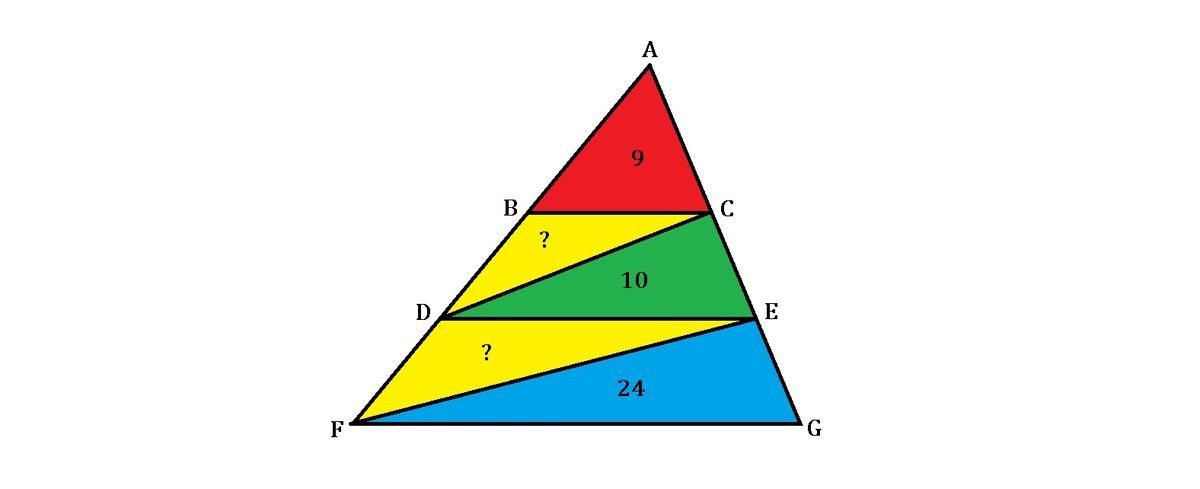
As shown above, △ A F G is partitioned into smaller ones with B C ∣ ∣ D E ∣ ∣ F G , and the number in each colored region indicates the area of that triangle.
What is the total area of the yellow region?
Note : Figure not drawn to scale.
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
very nice problem.
Did the same way! Great problem and solution
We note that △ A B C , △ A D E , and △ A F G are similar. Let B C = x , D E = y , and F G = z . Then the ratio of the three similar triangles is A A B C : A A D E : A A F G = x 2 : y 2 : z 2 . We can also consider the ratios of areas of the red, green, and blue triangles as follows:
x 2 y ( y − x ) ( x y ) 2 − x y − 9 1 0 ( x y − 3 5 ) ( x y + 3 2 ) ⟹ x y = A A B C A C D E = 9 1 0 = 0 = 0 = 3 5 Since x y > 0
Similarly,
x 2 z ( z − y ) ( x z ) 2 − x 2 y z ( x z ) 2 − 3 5 x z − 3 8 ( x z − 3 8 ) ( x y + 1 ) ⟹ x z = A A B C A E F G = 9 2 4 = 3 8 = 0 = 0 = 3 8 Since x z > 0
Now, we have A A B C A A D E = ( 3 5 ) 2 ⟹ 9 A B C D + 9 + 1 0 = 9 2 5 ⟹ A B C D = 6
Similarly, A A B C A A F G = ( 3 8 ) 2 ⟹ 9 A D E F + A A D E + 2 4 = 9 A D E F + 2 5 + 2 4 = 9 6 4 ⟹ A D E F = 1 5
Therefore A B C D + A D E F = 6 + 1 5 = 2 1 .
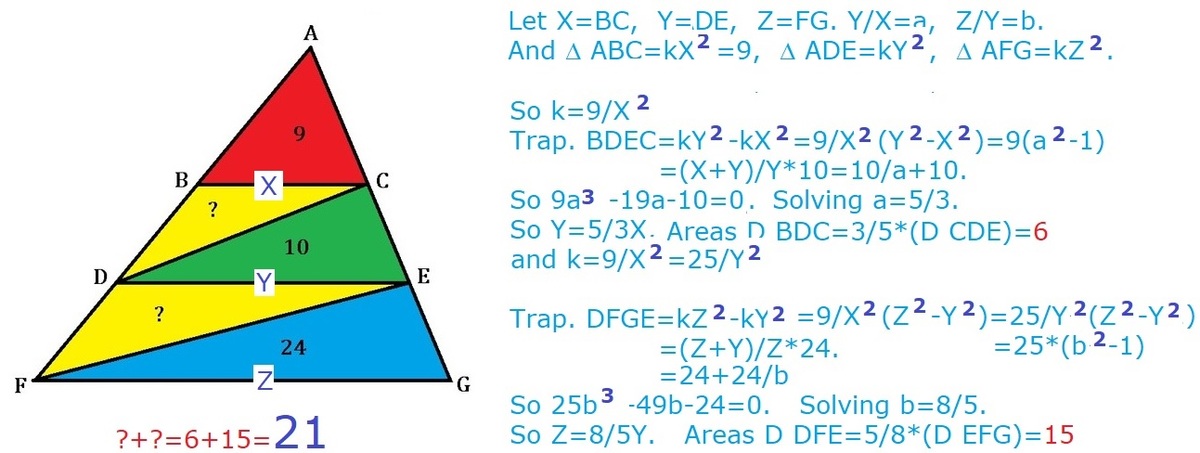
With B C ∣ ∣ D E ∣ ∣ F G , we can conclude that △ A B C ∼ △ A D E ∼ △ A F G .
Suppose the ratio of B C D E = x and that of B C F G = y for some positive numbers x , y .
We can then set up equations of the known area ratios:
x ( x − 1 ) ( 9 ) = 1 0
y ( y − x ) ( 9 ) = 2 4
Solving for x , we will obtain:
9 x 2 − 9 x − 1 0 = 0
( 3 x − 5 ) ( 3 x + 2 ) = 0
Thus, x = 3 5 . Substituting this into the second equation, we will obtain:
y ( 3 y − 5 ) = 8
3 y 2 − 5 y − 8 = 0
( 3 y − 8 ) ( y + 1 ) = 0
Thus, y = 3 8 .
Now we can calculate the area of △ B C D = 9 x 2 − 1 0 − 9 = 2 5 − 1 9 = 6 .
Then the area of △ D E F = 9 y 2 − 9 x 2 − 2 4 = 6 4 − 2 5 − 2 4 = 1 5 .
Finally, the total yellow area = 1 5 + 6 = 2 1 .