Triangle Centers
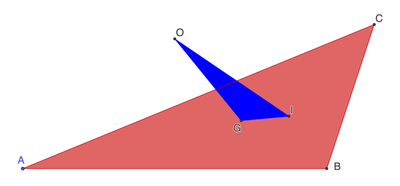
The sides of the red triangle are integers between and inclusive. The vertices of the blue triangle are formed by the incenter, circumcenter, and centroid of the red triangle. If the area of the blue triangle is expressed as , find its maximum value. Submit .
Note: As always, and are coprime and square-free.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the circumcentre 0 as the origin, if A , B , C have position vectors a , b , c respectively, then the position vectors of the centroid G and the incentre I are O G = 3 1 ( a + b + c ) O I = a + b + c 1 ( a a + b b + c c ) and hence O I × O G = 3 ( a + b + c ) 1 [ ( a − b ) a × b + ( b − c ) b × c + ( c − a ) c × a ] Thus the area of O I G is (here R is the radius of the circumcircle): ∣ O I G ∣ = ∣ ∣ ∣ ∣ 6 ( a + b + c ) R 2 [ ( a − b ) sin 2 C + ( b − c ) sin 2 A + ( c − a ) sin 2 B ] ∣ ∣ ∣ ∣ = 6 ( a + b + c ) R ∣ ∣ ∣ ( a − b ) c cos C + ( b − c ) a cos A + ( c − a ) b cos B ∣ ∣ ∣ = 2 4 ( a + b + c ) Δ a b c ∣ ∣ ∣ ∣ ( a − b ) c 2 a b a 2 + b 2 − c 2 + ( b − c ) a 2 b c b 2 + c 2 − a 2 + ( c − a ) b 2 a c a 2 + c 2 − b 2 ∣ ∣ ∣ ∣ = 4 8 ( a + b + c ) Δ 1 ∣ ∣ ∣ ( a − b ) c 2 ( a 2 + b 2 − c 2 ) + ( b − c ) a 2 ( b 2 + c 2 − a 2 ) + ( c − a ) b 2 ( a 2 + c 2 − b 2 ) ∣ ∣ ∣ = 1 2 1 ∣ ∣ ( b − a ) ( c − a ) ( c − b ) ∣ ∣ ( − a + b + c ) ( a − b + c ) ( a + b − c ) a + b + c where Δ = 4 1 ( a + b + c ) ( − a + b + c ) ( a − b + c ) ( a + b − c ) is the area of the triangle A B C . Thus ∣ O I G ∣ has been expressed in terms of the sides of the triangle A B C . Maximising this expression over the (finite) set of possible edge lengths { ( a , b , c ) ∈ N 3 ∣ ∣ 1 ≤ a ≤ b ≤ c ≤ 1 0 , c < a + b } , we see that the largest area of O I G is 6 7 7 , when a = 3 , b = 8 , c = 1 0 .
This makes the answer 7 − 6 = 1 .