Triangle-Ception I
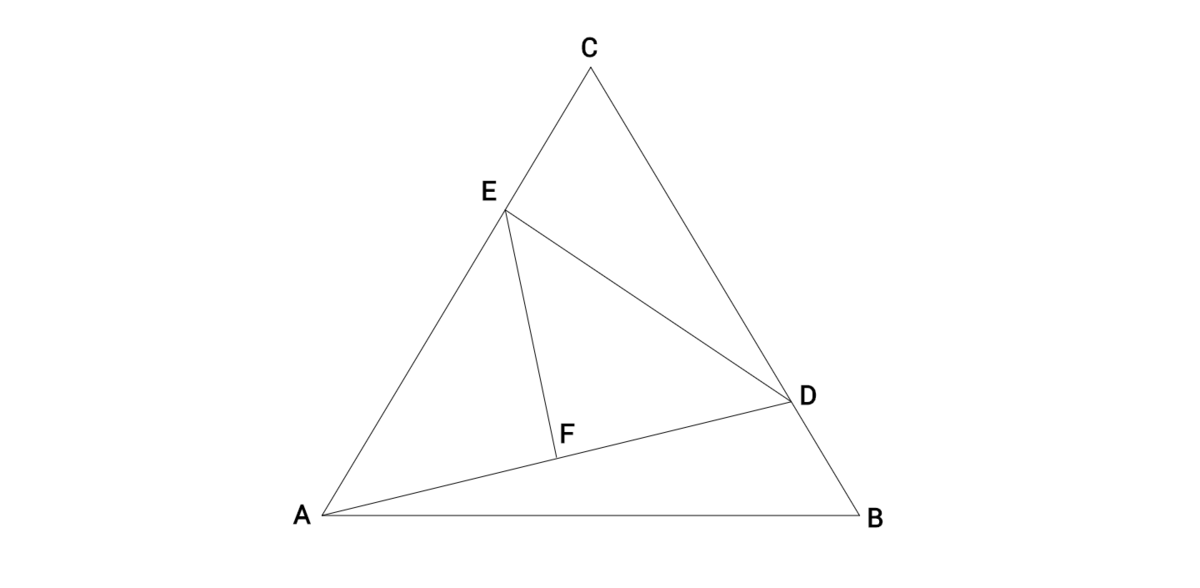
Equilateral triangle A B C has side lengths of 1 2 . A cevian A D is drawn from A to a point D on B C . A segment D E is then drawn from point D to a point E on A C . Lastly, a segment E F is drawn from point E to a point F on A D .
Given that the areas of triangles A B D , C D E , D E F , and A E F are all equal, the length of E F 2 is equal to q p where p and q are co-prime positive integers. Find the value of p + q .
The answer is 137.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Same Method
Nice solution. You used theorems, thats good.
What is Stewart Theorm?
Can you please explain how you got perfect fraction from square root of 117. Thanks.
Log in to reply
Going back to the Stewart's theorem section, we have ( 2 1 1 7 ) 2 × 1 1 7 + E F 2 × 1 1 7 = 2 1 1 7 × 6 1 2 + 2 1 1 7 × 8 2 . Multiplying everything out will give us an equation where every term has exactly one 1 1 7 , from which we can divide both sides by 1 1 7 , thus eliminating it from the equation.
We can also use co-ordinate geometry to solve this. I think it will be easier.
Did the same. Just used Appolonius theorem instead of Stewart's theorem since EF is a median. After all, great question and great solution.
Find DC=9,DB=3.EC=4,EA=8,AD^2=117, ED^2=61, using cosine theorem and area division in four equal parts.
Now use Pythagorean’s relation to find EF^2=133/4 and answer as 133+4=137
Let's start with determining where A D should intersect side B C . Since triangle A B D should have 4 1 the total area of the triangle, we can deduce using A r e a = 2 1 B a s e × H e i g h t that point D should be placed 4 1 of the way down side B C from vertex B .
The same reasoning can be used to to determine where segment D E should intersect side A C . We have a triangle A C D for which we need to divide into three triangles of equal area, so point E should be 3 1 of the way down side A C from vertex C .
Last, we can use once again the same reasoning from above to determine where segment E F should intersect segment A D . We need to split the remaining triangle A D E into two triangles of equal area, so point F should lie on the midpoint of A D .
Now that we know our ratios, lets put some numbers to the segments. Because our side lengths for the equilateral triangle are 1 2 ,
B D = 3 , C D = 9 , C E = 4 , A E = 8 .
Using Law of Cosines :
D E 2 = 4 2 + 9 2 − ( 2 ) ( 4 ) ( 9 ) cos ( 6 0 o ) D E = 6 1
Using Law of Cosines again, A D 2 = 3 2 + 1 2 2 − ( 2 ) ( 3 ) ( 1 2 ) cos ( 6 0 o )
A D = 1 1 7
Since F lies on the midpoint of A D ,
A F = D F = 2 1 1 7
We now have all the information for triangle A D E to use Stewart's Theorem , which yields us ( 2 1 1 7 ) 2 × 1 1 7 + E F 2 × 1 1 7 = 2 1 1 7 × 6 1 2 + 2 1 1 7 × 8 2 .
Solving for E F 2 gives us
E F 2 = 4 1 3 3
which certainly cannot be reduced. Our answer is then
1 3 3 + 4 = 1 3 7