Triangle-Ception IV
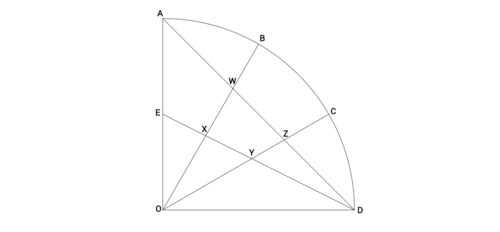 In the diagram above,
O
A
D
is a quarter circle of radius 2.
O
B
and
O
C
trisect arc
A
D
, and
D
E
bisects segment
O
A
. If the area of quadrilateral
W
X
Y
Z
can be expressed in the form
In the diagram above,
O
A
D
is a quarter circle of radius 2.
O
B
and
O
C
trisect arc
A
D
, and
D
E
bisects segment
O
A
. If the area of quadrilateral
W
X
Y
Z
can be expressed in the form
n m ( p − q r )
for positive integers m , n , p , q and r with g cd ( m , n ) = 1 , g cd ( p , q ) = 1 , and r is not divisible by the square of any prime. Find the value of
m + n + p + q + r .
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Great solution! Much more simple than mine!
And yeah... phones + latex never ends well...
I used coordinate geometry to solve the question, however my method is way too long and not appreciable enough to be shared. :|
First, lets break down the diagram into sections in order to get the area of W X Y Z . Let [ a ] denote the area of a .
We can tell by our diagram that
[ △ A O D ] = 2 = [ △ A W O ] + [ △ O Z D ] + [ △ O X Y ] + [ W X Y Z ]
We can also place O at the origin and let O A lie on the y − a x i s and O D lie on the x − a x i s .
We can represent every line that makes up W X Y Z on the diagram as:
O B = y 1 = 3 x O C = y 2 = 3 1 x A D = y 3 = 2 − x D E = y 4 = 1 − 2 1 x
We can find the areas of these triangles by dropping down perpendiculars and using A r e a = B a s e × H e i g h t
To find [ △ A W O ] we need the x-value of y 1 = y 3 , so we get
3 x = 2 − x x = 3 − 1
And by A r e a = B a s e × H e i g h t , we get
[ △ A W O ] = 2 ( 3 − 1 ) ( 2 ) = 3 − 1
To Find [ △ O Z D ] we need the y-value of y 2 = y 3 , so we get
3 1 x = 2 − x = y 2 = y 3 y 2 = y 3 = 3 − 1
And so we can conclude that
[ △ A W O ] = [ △ O Z D ] = 3 − 1
In order to find [ △ O X Y ] , we can see that
[ △ E O D ] = 1 = [ △ O X Y ] + [ △ E X O ] + [ △ O Y D ]
To find △ E X O , we need the x-value of y 1 = y 4 , so we get
3 x = 1 − 2 1 x x = 1 1 2 ( 2 3 − 1 )
So we can conclude that
[ △ E X O ] = 2 ( 1 1 2 ( 2 3 − 1 ) ) ( 1 ) = 1 1 1 ( 2 3 − 1 )
Also, to find [ △ O D Y ] , we need the y-value of y 2 = y 4 , so we get
3 1 x = 1 − 2 1 x = y 2 = y 4 y 2 = y 4 = 4 − 2 3
So we can conclude that
[ △ E X O ] = 4 − 2 3
Now we have everything we need to finish the problem. We get that
[ W X Y Z ] = 2 − [ △ A W O ] − [ △ O Z D ] − [ △ O X Y ] [ W X Y Z ] = 2 − [ △ A W O ] − [ △ O Z D ] − ( 1 − [ △ E X O ] − [ △ O Y D ] ) [ W X Y Z ] = 2 − ( 3 − 1 ) − ( 3 − 1 ) − ( 1 − ( 4 − 2 3 ) − ( 1 1 1 ( 2 3 − 1 ) ) )
After some manipulation we get that
[ W X Y Z ] = 1 1 2 ( 3 8 − 2 1 3 )
This satisfies all of our constraints for m , n , p , q , r , so
m + n + p + q + r = 2 + 1 1 + 3 8 + 2 1 + 3 = 7 5
Used the same method as Mahdi Al-kawaz . I was to give a little more detail. But I think his is sufficient.
However on second thought, coordinate geometry is also a nice method.
OD and OA, X and Y rectangular axis. Then,
Y
O
B
=
3
X
,
Y
O
C
=
3
1
X
,
Y
A
D
=
−
X
+
2
,
1
Y
E
D
+
2
X
E
D
=
1
.
Points of intersections give coordinates of W, X, Y, Z. So the area.
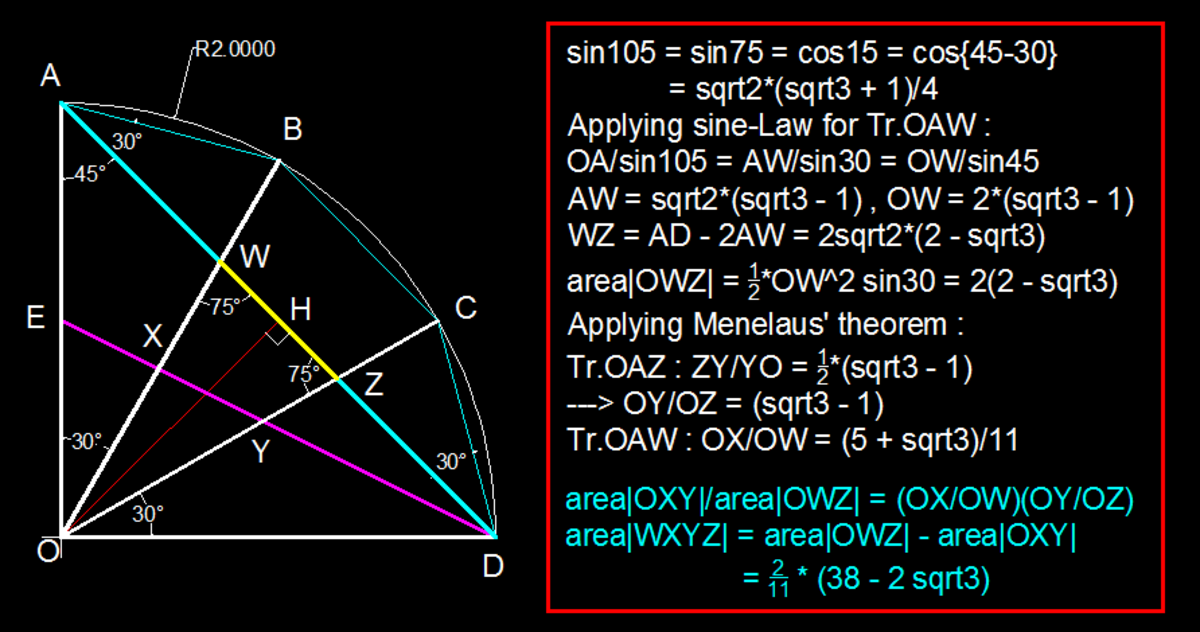
Using basic facts we can obtain the following:
∠ Z O D = ∠ W O Z = 3 0 ∘ , ∠ A D O = 4 5 ∘ , E D = 5 , sin E D O = 5 1 and O W = O Z .
let ∠ E D O = α ⇒
sin O Y D = sin ( 1 5 0 ∘ − α ) = 2 5 2 + 3
sin O X D = sin ( 1 2 0 ∘ − α ) = 2 5 1 + 2 3 .
Applying the law of sines on the triangles OWD, OXD and OYD we get O W = 1 + 3 4 ,
O X = 1 + 2 3 4 and O Y = 2 + 3 4 respectively.
The area of WXYZ=area of OWZ-area of XOZ = 2 1 × sin 3 0 ∘ × O W × O Z − 2 1 × sin 3 0 ∘ × O X × O Y = 1 1 2 ( 3 8 − 2 1 3 )
Conclusion 1. The answer is 7 5 .
Conclusion 2. Writing a solution using my phone..never again.