Triangle defined by one point
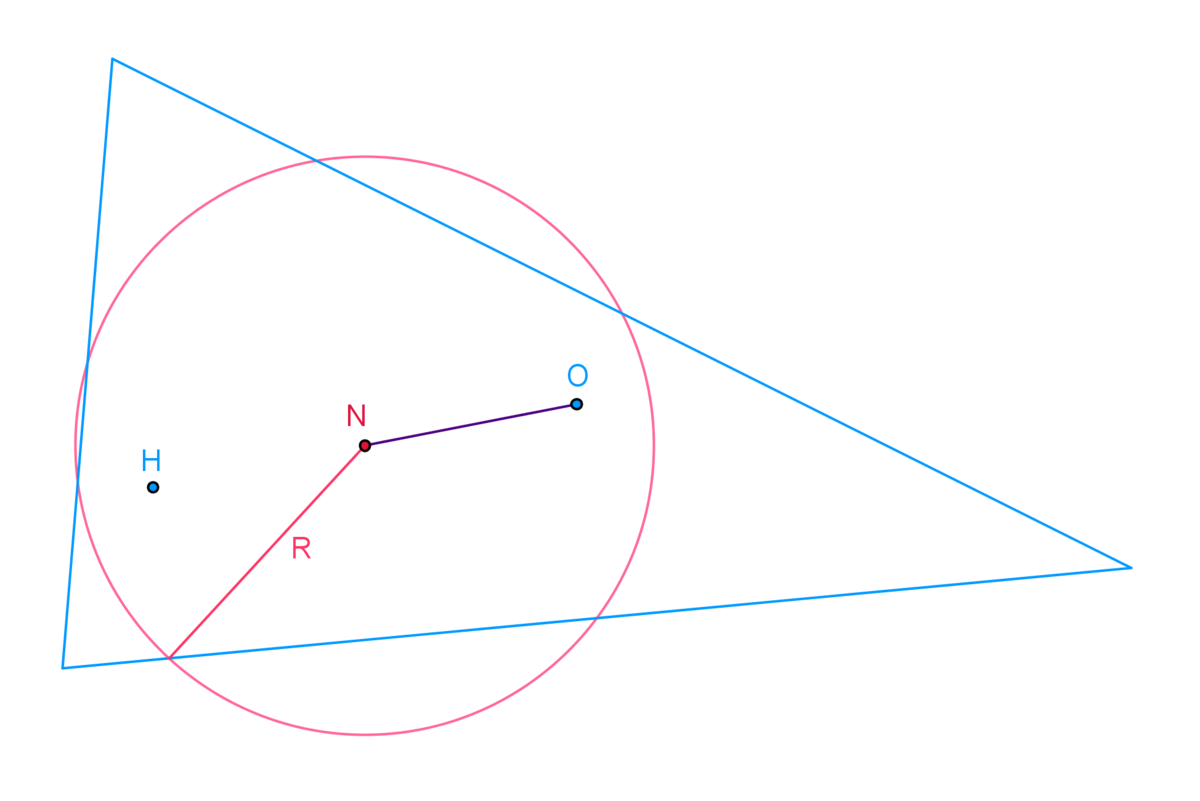
Point is an orthocentre of a triangle. Vertices of a triangle are on the axes of the coordinate system. is circumcentre of the triangle, is radius of triangle's nine point circle and is centre of the nine point circle.
Find
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let P denote the point of origin, A , B , C vertices of the triangle, R c its circumradius and a , b , c its side lengths.
Tetrahedron A B C P is trirectangular ⇒ orthogonal ⇒ P H ⊥ △ A B C .
Plane on which △ A B C lies can be found x + 2 y + 3 z = 1 4 and points A ( 1 4 , 0 , 0 ) , B ( 0 , 7 , 0 ) , C ( 0 , 0 , 1 4 / 3 ) .
Triangle's side lengths can be found using Pythagorean theorem, and the rest of the values using regular formulas. Heron's formula or de Gua's theorem to find triangle area and then:
R c = 4 △ A B C a b c
O H 2 = 9 R c 2 − ( a 2 + b 2 + c 2 )
R = R c / 2 , O N = O H / 2
Note:
As an additional exercise I got the following:
For H ( k , l , m ) plane has equation k x + l y + m z = k 2 + l 2 + m 2 .
Vertices: A ( a l , 0 , 0 ) B ( 0 , b l , 0 ) C ( 0 , 0 , c l ) a l = k k 2 + l 2 + m 2 , b l = l k 2 + l 2 + m 2 , c l = m k 2 + l 2 + m 2 )
Centroid: G ( 3 k k 2 + l 2 + m 2 , 3 l k 2 + l 2 + m 2 , 3 m k 2 + l 2 + m 2 )
Circumcentre : O ( 2 k l 2 + m 2 , 2 l k 2 + m 2 , 2 m k 2 + l 2 ) = O ( 2 a l − k , 2 b l − l , 2 c l − m )
Circumradius: R c 2 = ( ( a l 2 + b l 2 + c l 2 ) − ( k 2 + l 2 + m 2 ) ) / 4
O H 2 = ( a l 2 + b l 2 + c l 2 − 9 ( k 2 + l 2 + m 2 ) ) / 4
R c 2 − O H 2 = 2 ( k 2 + l 2 + m 2 ) = 2 H P 2
R c 2 + O H 2 = 2 O P 2
a l k = b l l = c l m = k 2 + l 2 + m 2