Triangle espacate
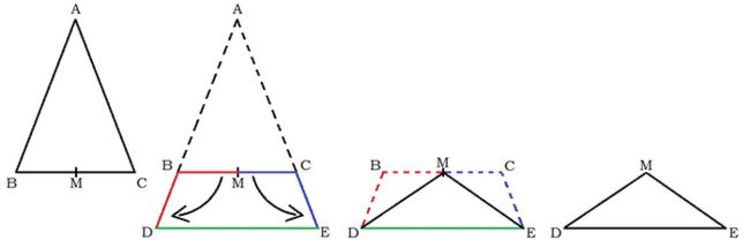 Look at the transformation the isosceles triangle
undergoes above.
and
are collinear, and so are
and
.
is the midpoint of
and
. Suppose we do the same thing with triangle
and so on, repeating the process indefinitely. How many times do we need to do this - including the first transformation - for the greater angle of the resulting triangle to be
?
Look at the transformation the isosceles triangle
undergoes above.
and
are collinear, and so are
and
.
is the midpoint of
and
. Suppose we do the same thing with triangle
and so on, repeating the process indefinitely. How many times do we need to do this - including the first transformation - for the greater angle of the resulting triangle to be
?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
DBM is isosceles and the external angle ∠ A B M is divided equally between ∠ B D M and ∠ B M D . Also, A, B and D are collinear, so are A, C and E, and B D = B M = C M = C E , so DE is parallel to BC. Hence, ∠ B M D = ∠ M D E = 2 ∠ A B M . The same goes for ∠ D E M . As a result, the congruent angles ( α n )of the resulting isosceles triangle is always half of those of the former ones ( α n − 1 ). Let ∠ A B M be α 0 . We know that ∠ B A C = 2 0 º . Thus:
α n = 2 α n − 1
α 0 = 8 0 º
α n = α 0 ⋅ ( 2 1 ) n
α n = 8 0 º ⋅ 2 − n
Let ∠ B A C be θ 0 , ∠ D M E be θ 1 and so on. Therefore, we have that:
θ n = 1 8 0 º − 2 ⋅ α n
θ n = 1 8 0 º − 2 ⋅ 8 0 º ⋅ 2 − n
For θ n = 1 7 5 º , it goes like this:
1 7 5 º = 1 8 0 º − 2 ⋅ 8 0 º ⋅ 2 − n
1 6 0 º ⋅ 2 − n = 5 º
2 − n = 3 2 1 = 2 − 5
n = 5
Hence, we need to form 5 triangles in order to get to the angle of 175º.