Triangle Formed By Intercepts
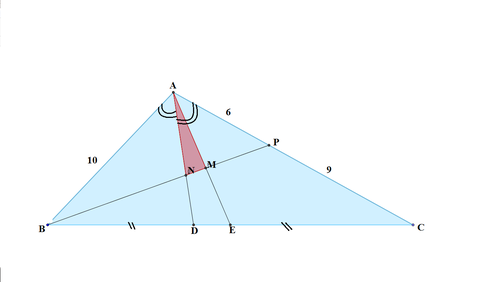 In
△
A
B
C
A
B
=
1
0
and
A
C
=
1
5
.
A
E
is the median from
A
and
A
D
is the internal bisector of
∠
B
A
C
. The point
P
is on
A
C
such that
A
P
=
6
.
B
P
intersects
A
D
at
N
and
A
E
at
M
. What is the value of
In
△
A
B
C
A
B
=
1
0
and
A
C
=
1
5
.
A
E
is the median from
A
and
A
D
is the internal bisector of
∠
B
A
C
. The point
P
is on
A
C
such that
A
P
=
6
.
B
P
intersects
A
D
at
N
and
A
E
at
M
. What is the value of
[ A N M ] [ A B C ] ?
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Not: there are other ways to compute M P B M . One of them is drawing a parallel parallel to B P through E . Let that line intersect A C at X . Now use midpoint theorem and similarity to arrive at M P B M = 2 5
Log in to reply
Thanks for this argument. My solution was very long, now I made a very better one.
Calculate the ratio of [AMN] and [ADE]. It's equal to AM/ME x AN/ND. Thus it's 5/14. Then calculate [ADE]/[ABC]. It's 1/10. Thus [AMN]/[ABC]=5/14 x 1/10=1/28.
can u clear my query ? by menelaus theorem the product should be -1 or 1 ??
Log in to reply
WE are not concerned with directed segments, we just require the numerical value for the measures of the lengths.
Applying Menelaus theorem in triangle AEC, with transversal PMB, you'll get M E A M = 3 4 Further, applying Menaluas in ADE with MNB transversal, we get N D A N = 3 5 The internal bisector theorem says that A C A B = D C B D = 3 2 , thus B D : D E : E C : : 4 : 1 : 5 (since E is the midpoint of BC) Thus [ N B D ] [ A N B ] = 3 5 Let it be 5x and 3x. Thus [ADB]=8x. Thus [ADE]= 2x (since, BD:DE=4:1) now [ A B E ] [ A B M ] = A E M A = 7 4 = ( 8 x + 2 x ) ( 5 x + [ A N M ] ) . Thus [ A N M ] = 7 5 x and [ A B C ] = 2 × [ A B D ] = 2 × 1 0 x = 2 0 x Thus [ A N M ] [ A B C ] = 7 5 x 2 0 x = 2 8
APB = 5 2 ABC
After much Calculation I Got AMB = 7 2 ABC
Also ANP = 2 0 3 ABC
So ANP + AMB - APB =( 7 2 + 2 0 3 ) ABC - 5 2 ABC
= ANM = 1 4 0 5 ABC
= A N M A B C = 5 1 4 0
= 28
apply Menalaus theorem 3 times to 3 triangles AEC with transversal MBP, ADC with transversal NBP and lastly, ANM with transversal BDE we can also find MN/BD. Note that suppose K is between A &B then ìf AK/KB=m then Ak/KB=m/m+1 and KB/AB=1/m+1 for faster calculation and to be beautiful geomatrics :D
Our aim is to find B P N M . Once we do that, we are done.How it will be clear later.
Apply Menelaus Theorem in △ B P C with A M E as transversal. We have A P C A × M B P M × E C B E = 1 .
Putting B E = E M and A P C A = 6 1 5 = 2 5 , we have M P B M = 2 5 ..... (i) As A D is the angle bisector of ∠ A , we have N P B N = 6 1 0 .......(ii)
Now assume B N = x , N M = y and M P = z .
From (i) we have z x + y = 2 5 ⟹ 2 x = 5 z − 2 y . . . ( v ) ⟹ 6 x = 1 5 z − 6 y . . . . ( i i i )
From (ii) we have y + z x = 6 1 0 ⟹ 6 x = 1 0 Y + 1 0 z . . . . . ( i v )
Equating (iii) and (iv) we have 1 0 z + 1 0 y = 1 5 z − 6 y ⟹ 5 z = 1 6 y = k . hence z = 5 k , y = 1 6 k .
Putting these values of y and z in (v) we have x = 1 6 7 k . Hence x : y : z = 3 5 : 5 : 1 6
Now [ A B P ] [ A N M ] = B P N M = x + y + z y = 3 5 + 5 + 1 6 5 = 5 6 5 . [ when two triangles have a common vertex, ratio of their areas is equal to ratio of their bases]
Hence [ A N M ] = 5 6 5 × [ A B P ] .
Again, [ A B C ] [ A B P ] = A C A P = 5 2 ⟹ [ A B P ] = 5 2 × [ A B C ]
therefore, [ A N M ] = 5 6 5 × 5 2 × [ A B C ] = 2 8 1 × [ A B C ]
Hence, [ A N M ] [ A B C ] = 2 8