Triangle Game
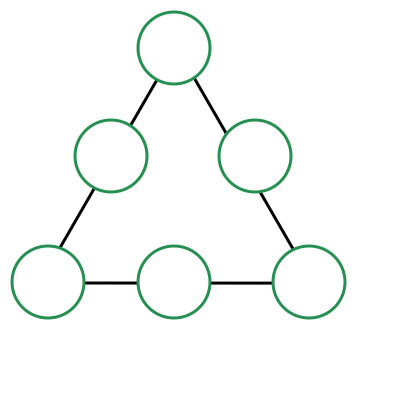 The numbers 1, 2, 3, 4, 5, 6 are written once in the circles above, such that each side of the triangle has the same sum.
The numbers 1, 2, 3, 4, 5, 6 are written once in the circles above, such that each side of the triangle has the same sum.
How many possibilities are there for the sum along the side?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the circles, starting at the top circle and going clockwise, ( a , b , c , d , e , f ) .
We wish to find all integer sums n such that
n = a + b + c = c + d + e = e + f + a .
Now 3 n = ( a + c + e ) + ( a + b + c + d + e + f ) = ( a + c + e ) + 2 1 .
Thus we are looking for n such that n = 7 + 3 a + c + e .
Now a + c + e can take on any value from 1 + 2 + 3 = 6 to 4 + 5 + 6 = 1 5 but what we require is that 3 ∣ ( a + c + e ) in order for n to be an integer. So at most we can have 4 possible sums, corresponding to a + c + e equalling 6 , 9 , 1 2 and 1 5 , giving us possible values for n of 9 , 1 0 , 1 1 and 1 2 .
We then need to confirm that these values are indeed possible, which they are using the following configurations for ( a , b , c , d , e , f ) :
( 1 , 5 , 3 , 4 , 2 , 6 ) ⟹ n = 9 ,
( 1 , 4 , 5 , 2 , 3 , 6 ) ⟹ n = 1 0 ,
( 2 , 3 , 6 , 1 , 4 , 5 ) ⟹ n = 1 1 ,
( 6 , 2 , 4 , 3 , 5 , 1 ) ⟹ n = 1 2 .
This confirms that there are indeed 4 possible sums.