Triangle Geometry
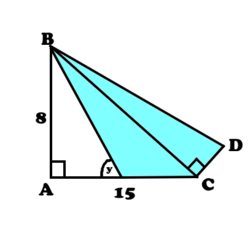 As shown in the diagram above,
and
. Also
and
. If
and
, what is the area (to the nearest unit) of the blue shaded triangles?
As shown in the diagram above,
and
. Also
and
. If
and
, what is the area (to the nearest unit) of the blue shaded triangles?
Diagram is not drawn to scale.
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Firstly, using Pythagoras' Theorem, we can say that: B C = 8 2 + 1 5 2 B C = 6 4 + 2 2 5 = 2 8 9 = 1 7 Therefore: △ B C D = 2 1 7 × 4 = 2 6 8 = 3 4 Now, using right-triangle trigonometry, we know that S i n ( θ ) = H O , therefore: s i n ( 5 3 . 1 ) = H 8 H = s i n ( 5 3 . 1 ) 8 = 1 0 Now if we call the angle at 53.1 point E, then: B E = 1 0 A E = B E 2 − A B 2 = 1 0 2 − 8 2 = 3 6 = 6 C E = 1 5 − A E = 1 5 − 6 = 9 △ B E C = 2 8 × 9 = 2 7 2 = 3 6 Therefore the area of the blue shade is: △ B C D + △ B E C = 3 4 + 3 6 = 7 0 Thank you to everyone who attempted my puzzle!