Triangle in a circle (vs triangle)
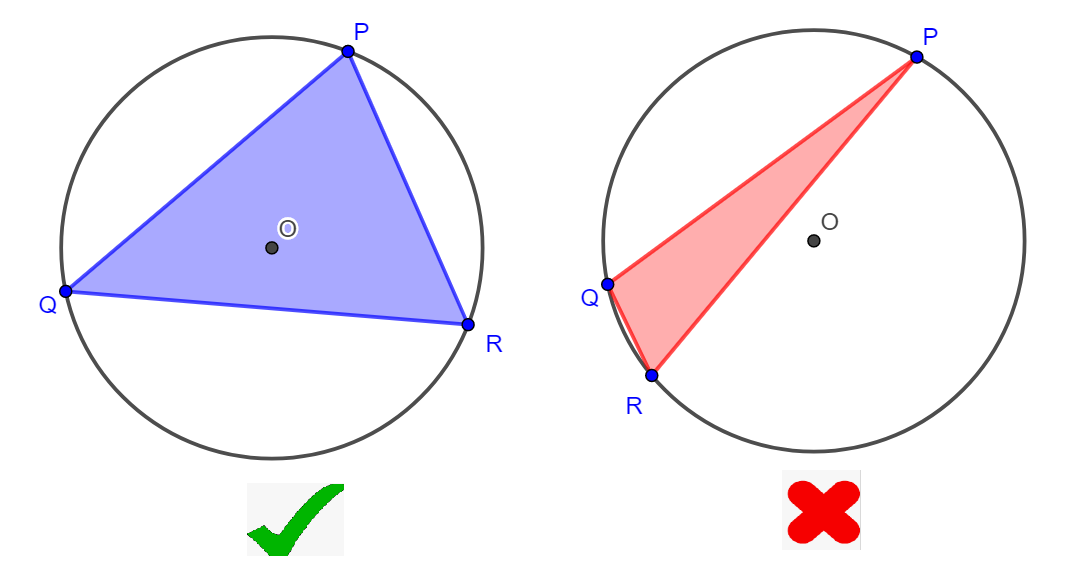 Three points, says
P
,
Q
and
R
are chosen uniformly at random from the circumference of a circle with centre
O
. Let
x
be the probability of triangle
P
Q
R
contains the point
O
. Find the value of
⌊
1
0
0
0
x
⌋
,
where
⌊
⋅
⌋
denotes the
floor function
.
Three points, says
P
,
Q
and
R
are chosen uniformly at random from the circumference of a circle with centre
O
. Let
x
be the probability of triangle
P
Q
R
contains the point
O
. Find the value of
⌊
1
0
0
0
x
⌋
,
where
⌊
⋅
⌋
denotes the
floor function
.
The answer is 250.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A very similar problem was posts about one month ago . I'll copy the relevant portion of my solution below.
Given two points
A
,
B
on a circle, the third point
C
must lie in the red region below if
△
A
B
C
is to contain the circle's center:
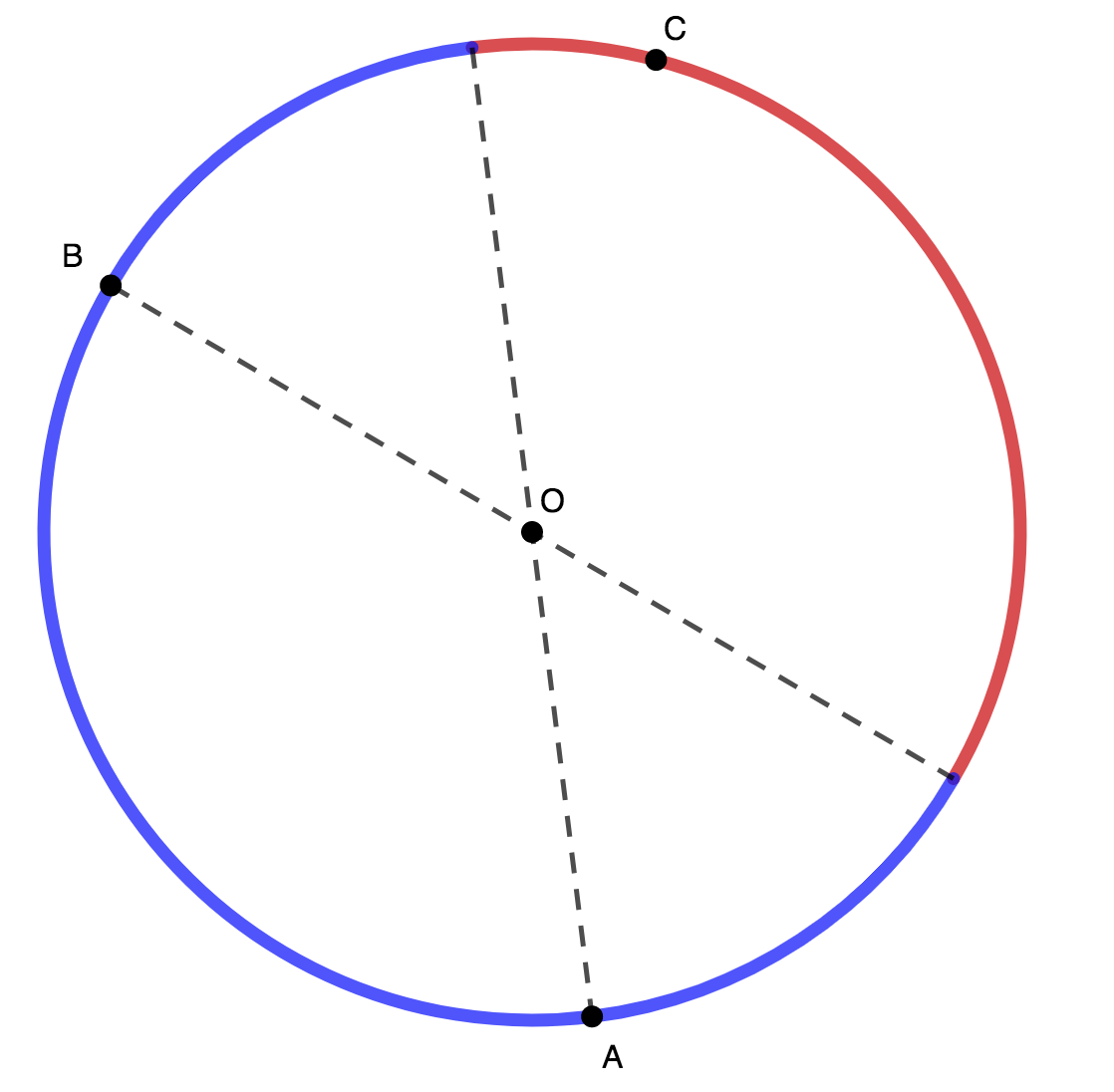
Now, we find the probability of this happening. Fix A and B on the circle, and let θ be the angle between them ( ∠ A O B ). Then 0 < θ ≤ π . Note that the angle intercepting the red region in the diagram is precisely θ . Thus the probability of a random point C being placed in the red area is 2 π θ . We integrate to compute the average probability over all possible θ : π − 0 1 ∫ 0 π 2 π θ d θ = π 1 [ 4 π θ 2 ] θ = 0 π = 4 π 2 π 2 = 4 1
⌊ 1 0 0 0 × 4 1 ⌋ = ⌊ 2 5 0 ⌋ = 2 5 0
Great answer! This is much easier to understand than Parth Sankhe's answer.
Probability is simply the probability of an acute triangle from 3 random points on a circle.
= π − 0 1 ∫ 0 π 2 π θ d θ = 0 . 2 5
Suppose P and Q placed randomly. Join the points P and O and extend it to the point A on the circumference. Do the similar to the segment Q O B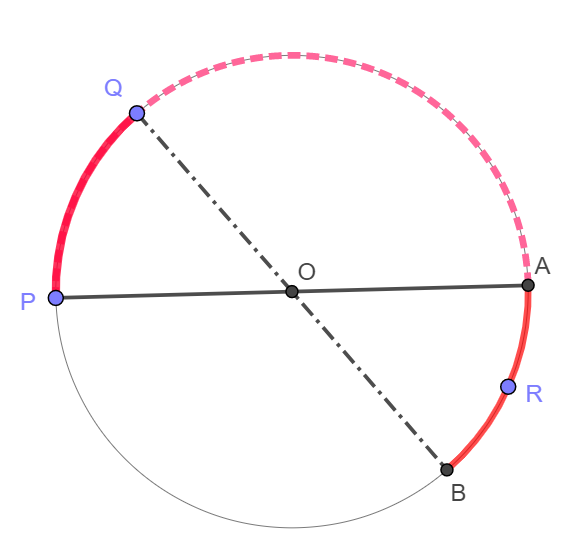
If the triangle P Q R contains the point O , then the final point R must be placed within the minor arc A B colored red (as shown). So the probability, x is the length of minor arc A B divided by the circumference. Suppose the circumference is of length 1 unit. Then x is the length of minor arc A B , which is the same as the length of minor arc P Q .
Now fix the point P and draw the segment P O A . By symmetry, the point Q is either above P A or below P A . Without loss of generality, let the point Q be above P A . As Q is chosen uniformly at random on the arc P A , averagely the point Q will fall on the center of the arc P A , which means that the length of minor arc P Q is 4 1 , and so the length of minor arc A B . This implies that x = 4 1 and hence ⌊ 1 0 0 0 x ⌋ = 2 5 0 .