Triangle In A Pentagon

Geometry Level 2

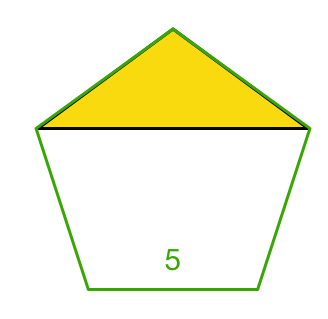
A regular pentagon with side length 5 is split into a quadrilateral and a triangle when two of the vertices are connected. What is the area of the triangle?

Give your answer to 2 decimal places.


The answer is 11.89.

View wiki
Janae Pritchett by Janae Pritchett

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Abc Xyz
Mar 8, 2016

Since it is a regular pentagon,the angles are 108 degrees and the sides are 5.

Therefore the area of the yellow triangle can be found with the 1 2 sin ⁡ θ × a × b \frac{1}{2} \sin \theta\times a \times b

Thus the answer is 1 2 sin ⁡ 108 × 5 × 5 \frac{1}{2}\sin 108\times 5\times 5 which comes to 11.89 \boxed{11.89} (approx).

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Ashutosh Malaviya
Mar 13, 2016

Theta = 108 degrees; Area of yellow triangle = (Height * Base)/2; Height = 5 Cos(Theta/2); Base = (5 Sin(Theta/2) + 5 Sin(Theta/2)); Area = (10 Sin(Theta/2)) (5 Cos(Theta/2))/2 = 25 Sin(54 degrees) Cos(54 degrees) = 11.87

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...