Triangle in a triangle (part 1)

Calculus Level 5

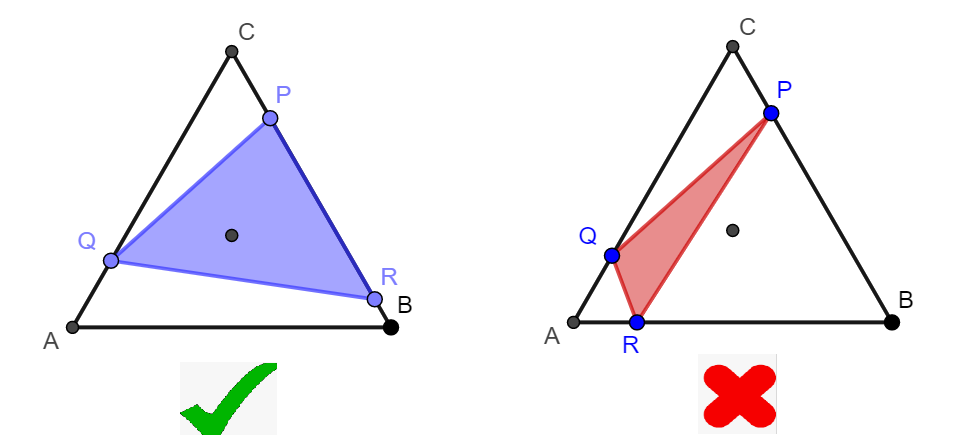
Three points, says $P, Q$ and $R$ are chosen uniformly at random from the perimeter of an equilateral triangle $ABC$ . Let $x$ be the probability of triangle $PQR$ contains the center of the triangle $ABC$ . Find the value of $\displaystyle\left\lfloor 1000x \right\rfloor,$ where $\lfloor \cdot \rfloor$ denotes the floor function .

**Note that the points $P, Q$ and $R$ are chosen from the $\bf{perimeter}$ , not inside the triangle.

Inspiration

The answer is 250.

1 solution

Chan Lye Lee
Nov 26, 2018

(Just realized that the following solution may be wrong as it may not guarantee the three points are chosen $\bf{uniformly}$ on the perimeter.Will update it again)

If we accept the answer to the problem https://brilliant.org/problems/triangle-in-a-circle-vs-triangle/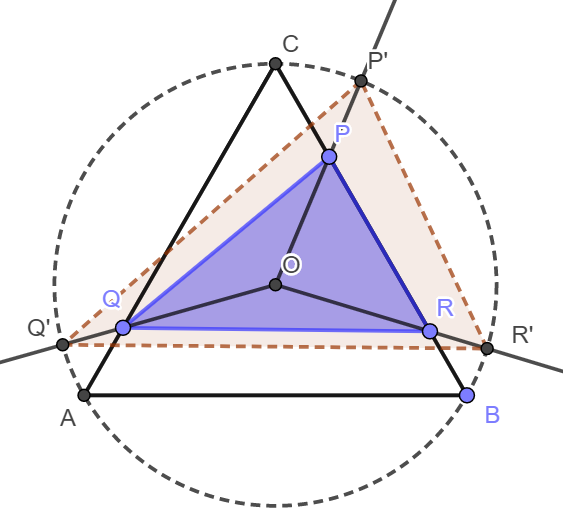

Then we see that there is a one-one corespondent for the point $P$ (from the perimeter of the equilateral triangle $ABC$ to the point $P'$ (from the circumference of the circle, as shown). Note that the triangle $PQR$ contains the center $O$ if and only if the triangle $P'Q'R'$ contains the center $O$ . Hence they have the same answer.

Triangle in a triangle (part 1)

The answer is 250.

1 solution

2 pending reports

Vote up reports you agree with