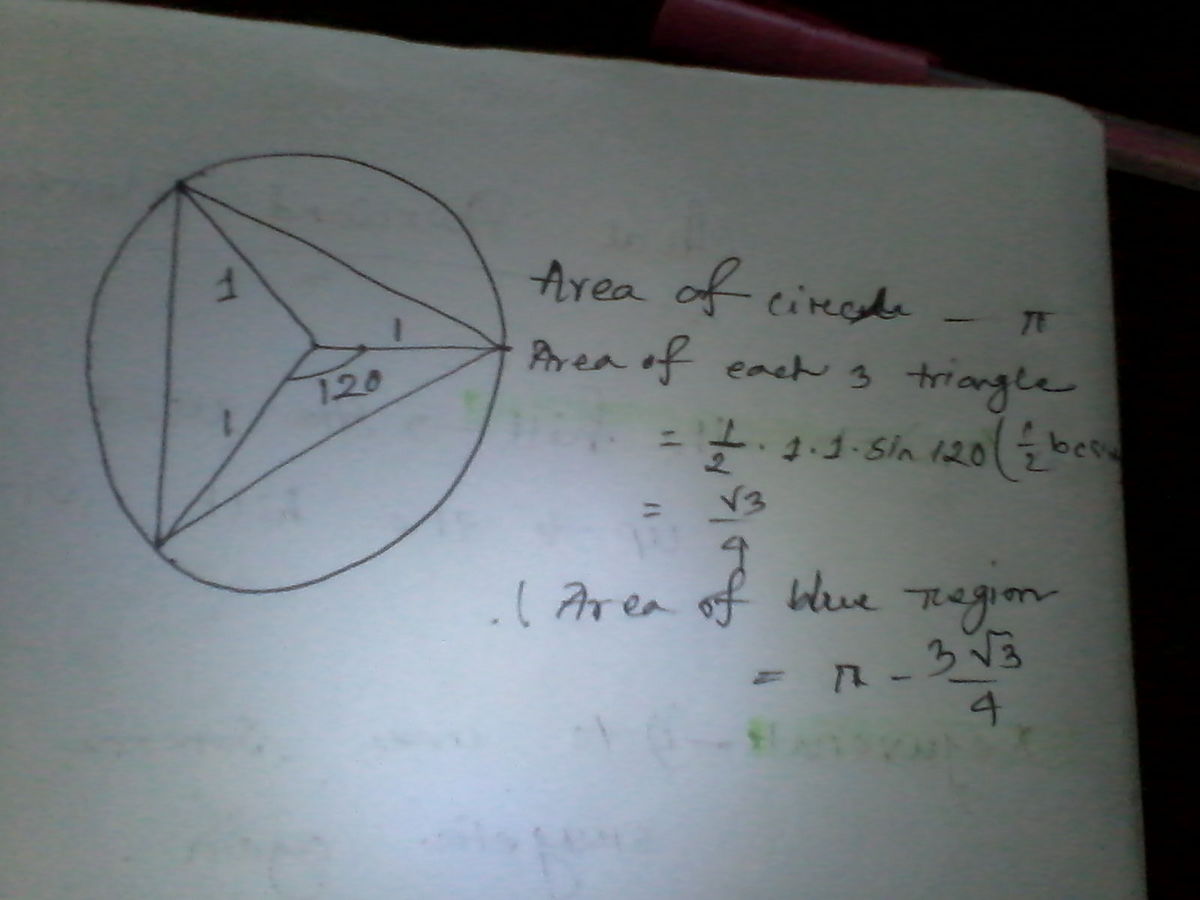Triangle In Circle

Join the center of the circle to each vertex of the triangle

Now , the red triangle consists of three congruent isosceles triangles.

Each isosceles triangle has two arms each of them equals the radius of the circle

and vertex angle 120

Area of each isosceles triangle = (1/2)(r^2) sin 120 = (1/4) (square root of 3)

Area of the red triangle = (3/4)(square root of 3)

Area of the circle = Pi

Then area of the blue region = Pi - (3/4)(square root of 3)

I used the fact that the circumcentre, centroid and orthocentre of an equilateral triangle are the same point, so the radius is 2/3 of the perpendicular height. Now using trigonometry $tan60 = \sqrt{3} = \frac{\frac{3}{2}}{x} \Rightarrow\ x = \frac{1}{2} \sqrt{3}$ $\therefore\ blue \ area = \pi - (\frac{3}{2} \times\frac{1}{2} \sqrt{3}) = \pi - \frac{3}{4} \sqrt{3}$

This was the second problem I did today about equilateral triangles that are inside a circle. I didn´t want to solve it with trig functions so I used only algebra and some triangle properties. So I derived a general formula and then replaced the radius variable with 1.

NO TRIGNOMETRY NEEDED

HERON'S FORMULA:-http://en.wikipedia.org/wiki/Heron%27s_formula

NOTE :- The third vertex of the triangle is C.