Triangle in Square

Let AN and DM intersect at R, BP and AN intersect at T and DM and BP intersect at S.

Its easy to get $AN=DM=BP=\frac { 5\sqrt { 5 } }{ 2 }$ by Pythagorean Theorem.

Also, $T$ is mid point of $AN$ and $BP$ , so $AT=\frac { 5\sqrt { 5 } }{ 4 } .$

Again, its easy to see that triangles $ADM$ , $ABN$ and $ABP$ are congruent, then $A\widehat { M } D=A\widehat { N } B=A\widehat { P } B$ and $A\widehat { D } M=B\widehat { A } N=P\widehat { B } A.$

Also $D\widehat { A } R=A\widehat { N } B$ because $AD//BC$ . As we know $B\widehat { A } N+A\widehat { N } B=90°,$ we can get $A\widehat { D } M+D\widehat { A } R=90°$ and because it, $AR$ and $DM$ are perpendiculars to each other. The good news is our desired triangle $RST$ is a right triangle!

Now, notice triangles $AMD$ , $RMA$ and $RAD$ are similars, so $\frac { AM }{ DM } =\frac { RM }{ AM } \Rightarrow { \left( \frac { 5 }{ 2 } \right) }^{ 2 }=RM\cdot \frac { 5\sqrt { 5 } }{ 2 } \therefore RM=\frac { \sqrt { 5 } }{ 2 }$

and

$\frac { AR }{ AM } =\frac { AD }{ DM } \Rightarrow 5\cdot \frac { 5 }{ 2 } =AR\cdot \frac { 5\sqrt { 5 } }{ 2 } \therefore AR=\sqrt { 5 } .$

By Menelau´s Theorem in triangle $AMB$ with $B$ , $S$ and $P$ in transversal line, we can find $MS$ :

$\frac { AB }{ BM } \cdot \frac { MS }{ SD } \cdot \frac { DP }{ PA } =1\Rightarrow \frac { 5 }{ \frac { 5 }{ 2 } } \cdot \frac { MS }{ \frac { 5\sqrt { 5 } }{ 2 } -MS } \cdot \frac { \frac { 5 }{ 2 } }{ \frac { 5 }{ 2 } } =1\therefore MS=\frac { 5\sqrt { 5 } }{ 6 } .$

Then, in triangle $RST$ , we have

$RS=MS-RM=\frac { 5\sqrt { 5 } }{ 6 } -\frac { \sqrt { 5 } }{ 2 } =\frac { \sqrt { 5 } }{ 3 }$

and

$RT=AT-AR=\frac { 5\sqrt { 5 } }{ 4 } -\sqrt { 5 } =\frac { \sqrt { 5 } }{ 4 }$

So, $[RST]=\frac { 1 }{ 2 } \cdot \frac { \sqrt { 5 } }{ 4 } \cdot \frac { \sqrt { 5 } }{ 3 } =\frac { 5 }{ 24 } .$

$$ Line $DM$ , $BP$ , and $AN$ can be represented as functions $$ $\begin{aligned} DM&&\Rightarrow &&y=2x\\ BP&&\Rightarrow &&2y=x+5\\ AN&&\Rightarrow &&2y=10-x\\ \end{aligned}$ $$ The intersection points those three lines are $\left(\dfrac{5}{3},\dfrac{10}{3}\right)$ , $\left(\dfrac{5}{2},\dfrac{15}{4}\right)$ , and $(2,4)$ . Thus, by using Wolfram Alpha , the area of the triangle bounded by the lines $DM$ , $BP$ , and $AN$ is 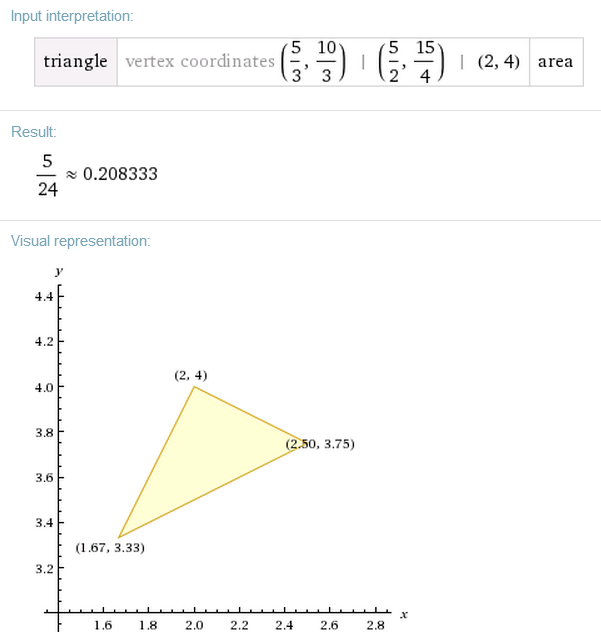$$ Triangle in Square Therefore, $p+q=\boxed{29}$ .

The area of all the given triangles viz ABN,AMD,APB is same i.e. in the form of p/q.The side of the square is 5 and it's mid-point is 2.5 therefore,the area of each triangle given above is 1/2 2.5(height) 5(side)=125/20 =25/4.The required answer is p+q i.e 25+4=29.

$\text{Let, AN and BP intersect at O, AN and DM intersect at F, DM and BP intersect at E.}$ $\text{In }\bigtriangleup NAB\text{, }\tan \angle NAB =\frac{1}{2}\text{ and }\angle NAB = \angle PBA\text{ ; }angle ANB = \angle OBN=\frac{\pi}{2}-\angle NAB$ $\text{Therefore, AO=OB=ON=OP=}\frac{AN}{2}=\frac{AB}{2 \cos \angle NAB}=\frac{5\sqrt{5}}{4}$ $\text{ and }\angle NOB=\pi-2 \angle OBN =2\angle NAB$ . $\text{In, }\bigtriangleup AMF\text{ we have, AF=}AM\cos \angle NAB=\sqrt{5} \text{. Therefore, OF=OA-AF=}\frac{\sqrt{5}}{4}$ $\text{In, }\bigtriangleup OEF\text{ we have, }\angle EOF =\angle NOB\text{ and, OE=OF} \tan \angle NOB=\frac{\sqrt{5}}{3}$ $\text{Thus, area of }\bigtriangleup OEF =\frac{OE\times OF}{2} =\frac{5}{24}$ $\text{Therefore p+q=}\boxed{29}$

Use co ordinate geometry guys, find the eqn. of 3 line that form the triangle and the intersections pts. are (2,4),(5/3,10/3),(5/2,15/4). Find the area of triamgle and solve this problem

Area of any triangle= (1/2)(5)(5/2) =25/4 =p/q =25+4 =29