Triangle Inscribed In Circle

Let $A$ and $B$ be fixed on a circle, Let $C$ be a third point on the circle and let $D$ be on $\overline{AB}$ such that $\overline{AB}\perp\overline{CD}$ . See the diagram below.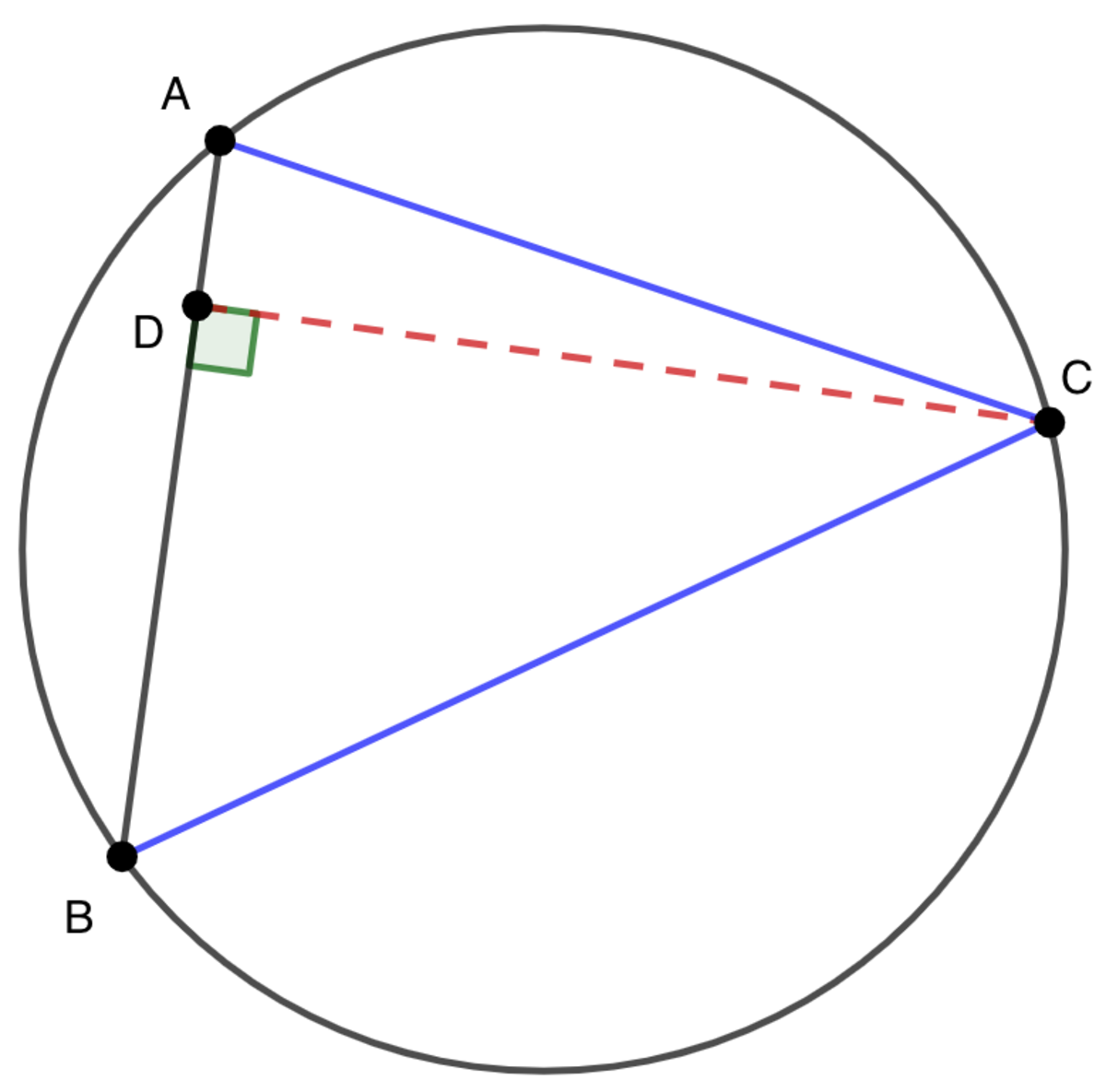 The area of $\triangle ABC$ is $\frac{1}{2}AB\cdot CD$ . We now attempt to maximize this area. For fixed $A$ and $B$ , this will be maximized when $\overline{CD}$ is at it's maximum length. This will occur when $C$ lies along the same diameter as the midpoint of $AB$ -- in other words, when $\overline{CD}$ is the perpendicular bisector of $\overline{AB}$ . This implies that $\triangle ABC$ is isosceles and, therefore, $\angle A \cong \angle B$ . By symmetry, it must be that $\angle A \cong \angle B \cong \angle C$ and $\triangle ABC$ is equilateral.

Assuming that $\triangle ABC$ is equilateral, we calculate its area. Since the equilateral triangle has side length $\sqrt{3}R$ (if you're not sure why, apply law of cosines to $\triangle OBC$ in the diagram below).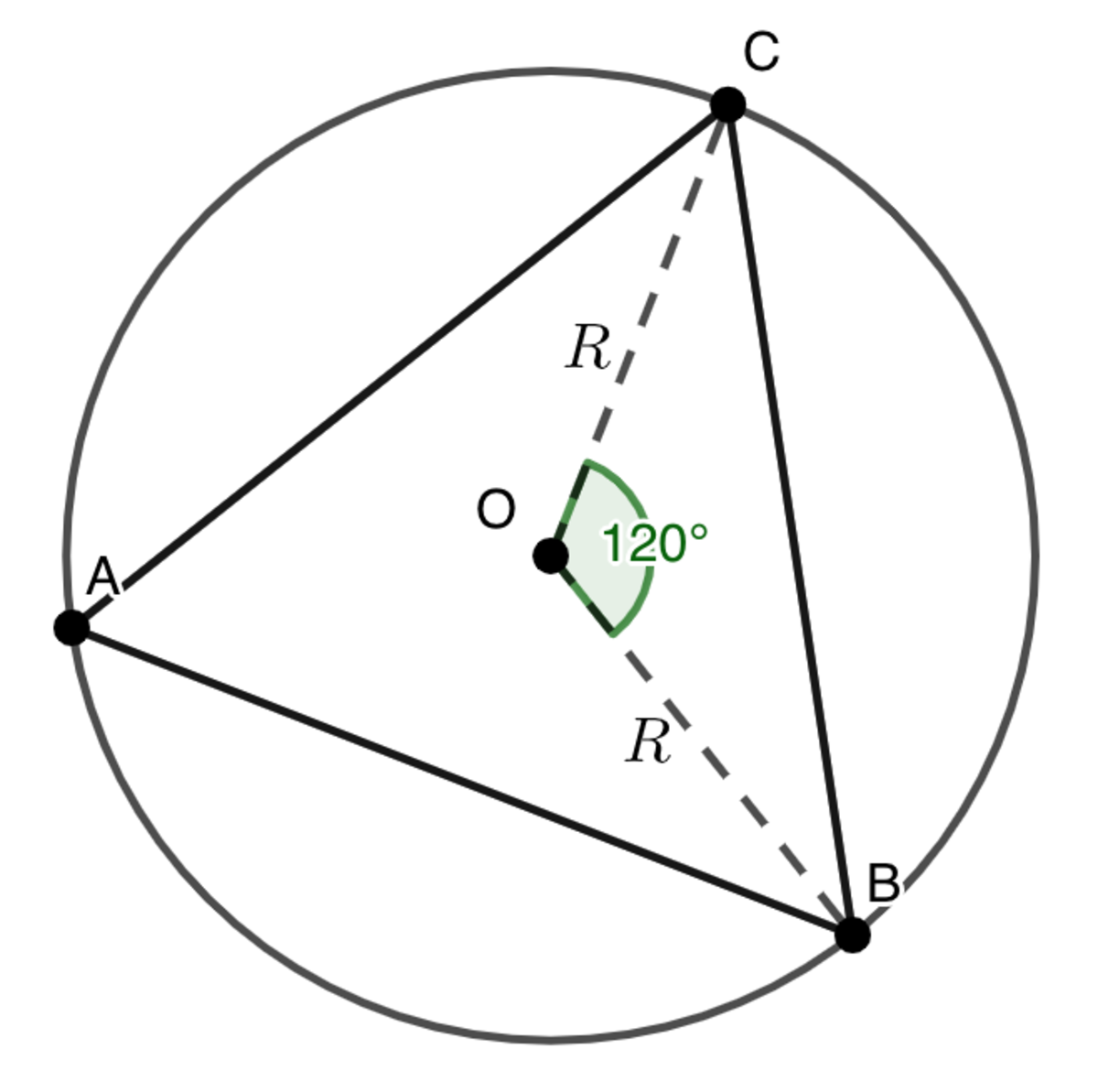 Thus, $\text{Area}(\triangle ABC = \frac{1}{2}(AC)(BC)\sin\angle C = \frac{1}{2}(\sqrt{3}R)(\sqrt{3}R)\sin 60^\circ = \frac{3}{2}R^2\cdot\frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{4}R^2$

Note that $\frac{3\sqrt{3}}{4} < \frac{3\cdot 2}{4} < \frac{3}{2} <\frac{\pi}{2}$ . This means that $\frac{3\sqrt{3}}{4}R^2 < \frac{\pi R^2}{2}$ .

We have just shown that the largest possible inscribed triangle is smaller than $50\%$ of the whole circle. So $\boxed{0\%}$ of inscribed triangles are at least half the circle's area.