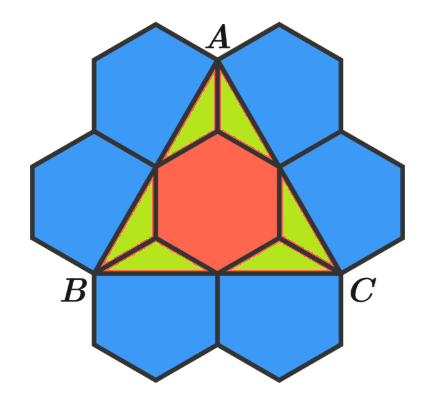
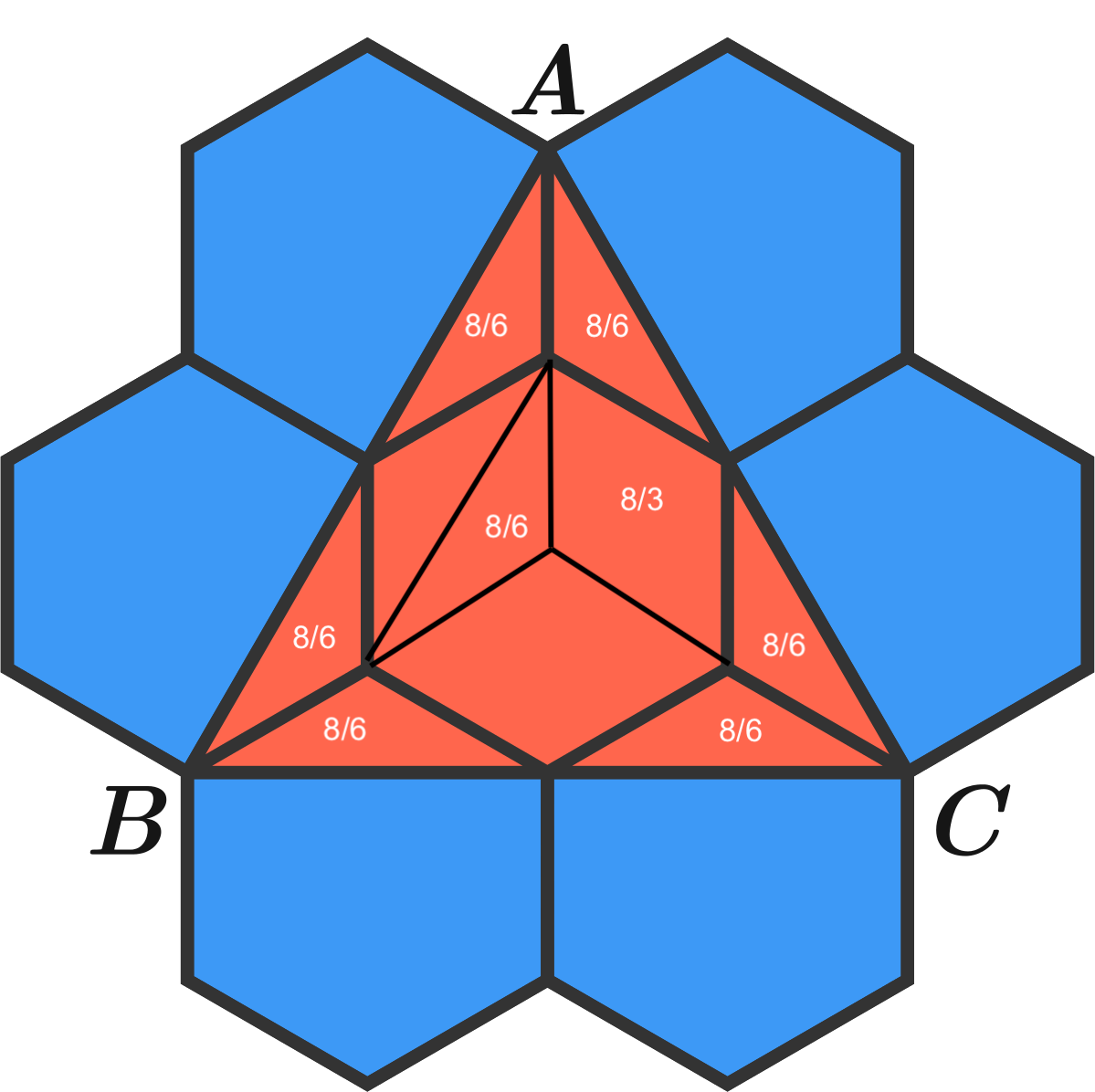
Triangle Inscribed In Hexagons
Seven identical regular hexagons are arranged in a honeycomb pattern.
If each hexagon has an area of 8 , then what is the area of △ A B C ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
How do you know the 6 pieces make exactly one congruent hexagon?
Log in to reply
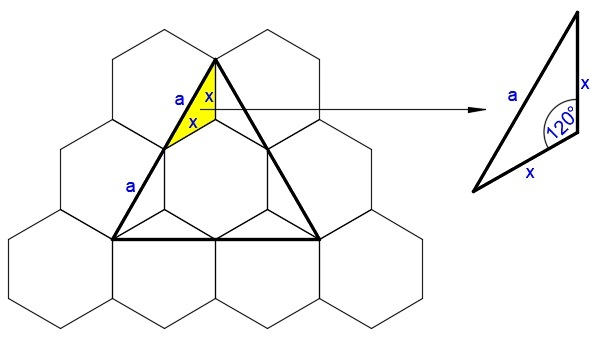
The leg of each isosceles triangle is the same as the side of the each regular hexagon, and the base of each isosceles triangle is the same as the diagonal between alternate points of each regular hexagon.
The vertex angle of each isosceles triangle is the same as the interior angle of each regular hexagon, and since 3 hexagons tile the space around a point, 3 vertex angles will also tile the space around a point.
Also, the 2 base angles of each isosceles triangle are the same as the interior angle of an equilateral triangle, and since 2 equilateral triangle angles can fill the space of an interior angle of a regular hexagon, 4 base angles will also fill the space of an interior angle of a regular hexagon.
This should be sufficient information to show that the 6 isosceles triangle pieces can make one congruent hexagon.
Log in to reply
Thank you for the explanation :)
This is an incredible explanation. I had to read it a couple times, but then it clicked and your words could not have been clearer or more elegant. Thank you.
This is also how I solved it.
wow, I screwed myself doing trigonometry and we could actually do this...
I had the same reasoning but I was wrong when I placed the 6 triangular pieces.
 The area of a regular hexagon is given by
A
H
=
2
3
3
x
2
where
x
is the side length. Substituting, we have
The area of a regular hexagon is given by
A
H
=
2
3
3
x
2
where
x
is the side length. Substituting, we have
8 = 2 3 3 x 2
x 2 = 3 3 1 6
Applying cosine rule, we have
a 2 = x 2 + x 2 − 2 x 2 cos 1 2 0 = 2 x 2 − 2 x 2 ( 2 − 1 ) = 3 x 2 = 3 ( 3 3 1 6 ) = 3 1 6
a = 3 1 6
The side of the equilateral triangle is 2 a .
2 a = 2 3 1 6
Let the side length of the equilateral triangle be y = 2 a = 2 3 1 6 . The area of an equilateral triangle is given by A = 4 3 y 2 where y is the side length. Substituting, we have
A = 4 3 ( 2 3 1 6 ) 2 = 4 3 [ 4 ( 3 1 6 ) ] = 1 6
Marvin
I simplified that entire process into 8+8. I mean you could do all that, but I'd choose to just move on with my life. If my process didn't work, then I would move on to the next quickest process, I'm sure that what you're doing though is quite the healthy brain exercise before the intermediate and advanced problems.
Log in to reply
I also did the same!!
This is really good man it´s well detailed
I had a similar start using the area of hexagon to obtain x^2. However , I proceed by using Area of triangle=0.5absinc which in this case , The area of 6 similar triangle outside of hexagon=0.5(x^2)sin120times6=8 then, 8+8=16
We divide the inner hexagon as well as triangle A B C into congruent isosceles triangles as shown above on the right. Since the inner hexagon is made up of six of these isosceles triangles, and triangle A B C is made up of twelve, the area of triangle A B C must be twice the area of the inner hexagon, i.e. 1 6
Hello! This problem has been changed since you've written your solution. I wanted to give you a chance to edit your solution before this problem is featured.
Log in to reply
Thanks for that; saw the note a bit too late, but I've made the necessary change.
Quite elegant!
That’s how I solved it.
In the first of the pictures below, it is shown that the area of a regular hexagon can be split up into thirds, and the second picture then shows that the area of a hexagon can be split up into sixths, by lines such as the blue ones.
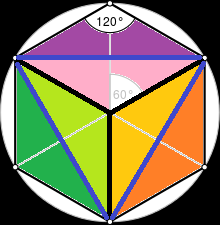
Therefore, as shown below, the area of triangle ABC is composed of one red hexagon, and six green triangles, each one of which has 6 1 of the area of each rectangle.
⟹ △ A B C = 1 ( 8 ) + 6 ( 6 1 × 8 ) = 8 + 8 = 1 6
1/6 apne kaise liya hai
The figure above shows that each isosceles triangle (in red) is 6 1 of a hexagon. Since △ A B C consist of six of these and one hexagon, the area of A B C is equal to the area of two hexagons, 1 6
Note that two small red triangles combine to give a third of the hexagon so it takes six such triangles to give a hexagon. Note that we have six red triangles which can give another hexagon. Thus the red region is just twice the area of a hexagon - 2 × 8 = 1 6 .
Moderator note : This solution is a bit out-of-date after Brilliant staff made some edits to this problem. The method for re-arranging the pieces is still valid, however!
As shown above, label points D , E , and F where Point D is the midpoint of A C , Point E is the center of △ D E F , and Point F is the midpoint of A D .
Now, to solve this problem, consider △ A B C to be equilateral because of the fact that all three of its side lengths are the sum of two congruent hypotenuses of two congruent isosceles triangles. Furthermore, consider △ D E F being a 3 0 ° − 6 0 ° − 9 0 ° triangle because E F is drawn perpendicular to A D and ∠ D E F is 6 1 of 3 6 0 ° . We can use this information to solve for D F as such
D F = 2 E F × 3
∴ D F = 2 1 × 3 ⇒ D F = 2 3
Now that we have solved for D F , we can solve for A C using midpoints F and D as such:
A C = A D × 2
A D = D F × 2
∴ A C = D F × 4 ⇒ A C = 2 3 × 4 ⇒ A C = 2 3
Now that we have solved for A C , we can compute the area of equilateral △ A B C as such:
Area of Equilateral Triangle = 4 s 2 3
∴ A △ A B C = 4 ( 2 3 ) 2 3 ⇒ 4 1 2 3 ⇒ 3 3 ⇒ A △ A B C ≈ 5 . 1 9 6
Your answer is quite different,everyone answer 16,not 5.196
Log in to reply
The Brilliant staff modified the problem which ultimately changed the answer. The original answer was 5.196.
Divide the triangle into four component triangles of equal area by joining the corners of the central hexagon which are at the midpoint of each side of the large triangle. If each 1/3 of the three small triangles has area x, the central triangle has area 3x, therefore x = 8/6. The total area = 12x = 12 x 8/6 = 16
In the triangle ABC there are 6 small triangles next to the hexagon
If we look at a hexagon, we see that 2 small triangles make up half the area of a hexagon
The area of a hexagon consists of 2/3 of the rectangle and one third of the two small triangles. A small triangle corresponds to 1/6 of the area of the hexagon. 6 small triangles correspond to the area of a hexagon. Therefore the area of the triangle ABC is 8 + 8 = 16
Ye kaise hoga whole solution dijiye
Area of a regular hexagon will be given by
(1/2)×b×h + (1/2)×b×h + b×B = 8
~ b×h + B×h = 8
~b(h+H) = 8
Now area of the triangle is given by
(1/2)×2b×(B+B+h+h)
~ (1/2)×2b×2(B+h)
~ 2b×(B+h) = 2×8 = 16
The hexagon is composed of six equilateral triangles each of area [sqrt(3)/4]s^2. Therefore, 6 (sqrt(3)/4)s^2 = 8, and s^2 = (16/9)sqrt(3). The triangular pieces each have an area equal to (1/2)(s^2)sin(120) = (1/2)(16/9)(sqrt(3) sqrt(3)/2 = 4/3. Then the red area = 6*(4/3) + 8 = 16. Ed Gray
The area if the red triangle equals 1 hexagon plus x (6 small triangles). Shift the red triangle down by the side length of the hexagon. Then you see that the area of the red triangle equals 3 hexagons minus x. Thus, x = 1. The red triangle equals 2 hexagons; hence, has area 16.
There is one hexagon and six hexagon peices in the triangle giving you a total area of 16
The area of the hexagon( A H e x a g o n ) is 2 3 a 2 3 ,the area of the hexagon in the picture is 8.So,we have
2 3 a 2 3 = 8 so a 2 = 3 3 1 6
Because each three small triangle( 3 × A s m a l l − △ ) in the picture is 3 6 0 ∘ degree so each ( A s m a l l − △ ) have one 1 2 0 ∘ .
.Let call b is 2 1 the side of the big triangle.Use the cosine rule,we have
b 2 = 2 a 2 − 2 a 2 cos 1 2 0 = 2 a 2 − 2 a 2 × 2 − 1 = 2 a 2 − − a 2 = 2 a 2 + a 2 = 3 a 2 = 3 × 3 3 1 6 = 3 1 6 so b = 3 1 6
So the side of the big triangle( A b i g − △ ) is
2 b = 2 × 3 1 6
The area of the equilateral triangle is 4 a 2 3 ,So the area of the ( A b i g − △ ) is
4 ( 2 a ) 2 3 = 4 4 a 2 3 = a 2 3 = ( 3 1 6 ) 2 3 = 3 1 6 × 3 = 1 6
The 6 triangular pieces can be moved to form a second congruent hexagon:
and since 1 hexagon has an area of 8 , 2 hexagons have an area of 1 6 .