Triangle Inside a Hexagon
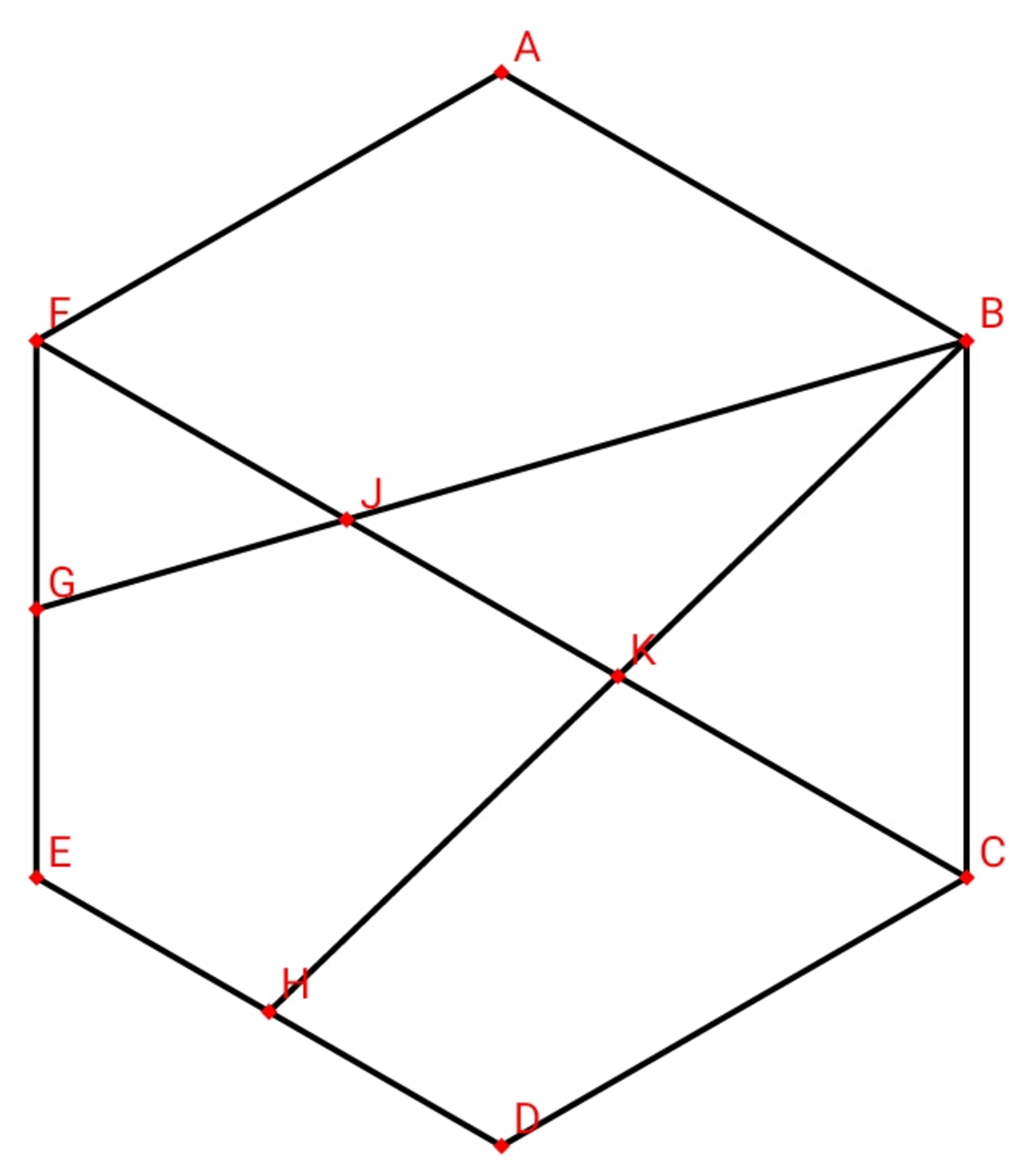
is a regular hexagon with . Point lies on such that . Point lies on such that . Diagonal intersects segment at and intersects at . Find the area of (in ) to two decimal places.
For more problem about hexagon, you may click here
Try another problem on my new set! Warming Up and More Practice
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
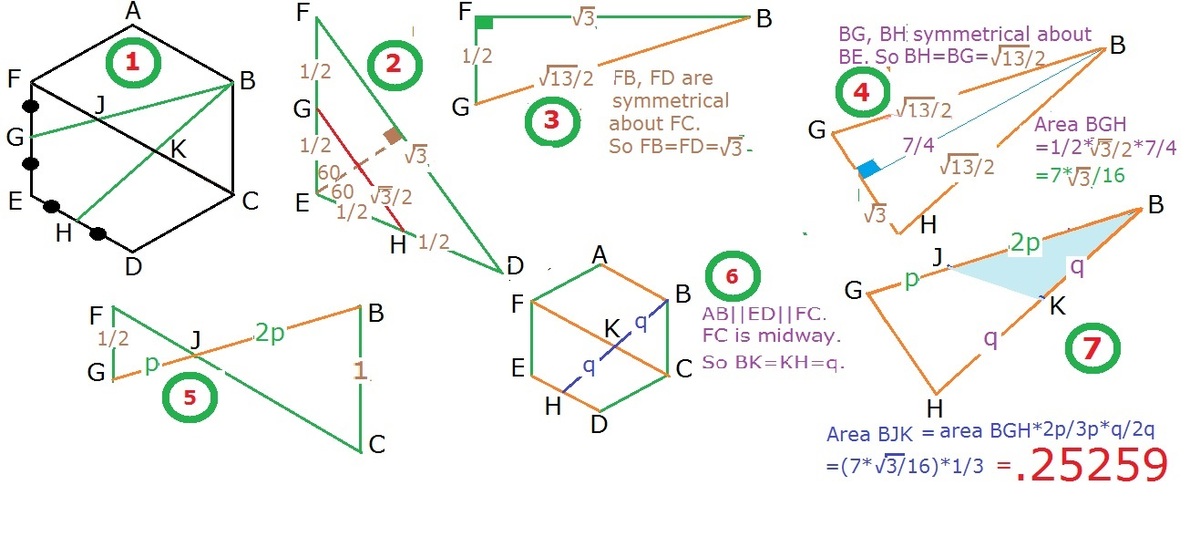
Since the regular hexagon with is made up of 6 equilateral triangle of the same side length. It can easily see that diagonal C F = 2 .
We note that △ B C J and △ G F J are similar. Therefore F J C J = G F B C = 2 , ⟹ C J = 2 F J . Since C F = 2 , ⟹ C J = 3 4 .
Now, we connect B D which intersects C F at L . Again, we note that △ B K L and △ B H D are similar and H D K L = B D B L = 2 1 , ⟹ K L = 2 1 H D = 4 1 .
Now the area of △ B J K is given by:
[ B J K ] = 2 J K ⋅ B L = 2 ( C J − K L − L C ) sin 6 0 ∘ = 2 ( 3 4 − 4 1 − cos 6 0 ∘ ) sin 6 0 ∘ = 4 8 7 3 ≈ 0 . 2 5