Right Triangle Tucked Into A Square

Geometry Level 1

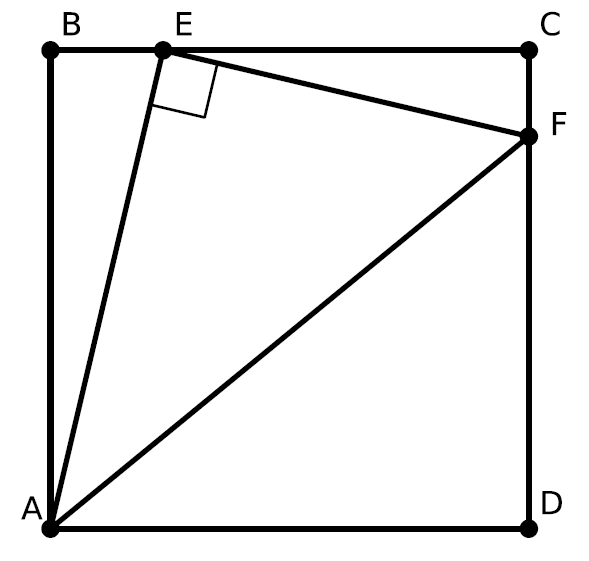
In the drawing above, $ABCD$ is a square. Points $E$ and $F$ are on $BC$ and $CD$ such that $AEF$ is a right triangle with $AE=4$ and $EF=3$ . What is the area of the square?

16

256

\frac{256}{17}

\frac{17}{16}

\frac{16}{17}

7 solutions

Brian Charlesworth
Feb 27, 2016

Note first that triangles $\Delta ABE$ and $\Delta ECF$ are similar. This implies that

$\dfrac{|AB|}{|AE|} = \dfrac{|EC|}{|EF|} \Longrightarrow \dfrac{|AB|}{4} = \dfrac{|EC|}{3} \Longrightarrow |EC| = \dfrac{3}{4}|AB|$ .

Next, by Pythagorean theorem , since $|AB| = |BC|$ , we have that $|AE|^{2} = |AB|^{2} + |BE|^{2}$

$\Longrightarrow 4^{2} = |AB|^{2} + (|BC| - |EC|)^{2} = |AB|^{2} + \left(|AB| - \dfrac{3}{4}|AB|\right)^{2}$

$\Longrightarrow 16 = |AB|^{2} + \dfrac{1}{16}|AB|^{2} = \dfrac{17}{16}|AB|^{2} \Longrightarrow |AB|^{2} = 16*\dfrac{16}{17} = \dfrac{256}{17}$ .

But the area of the square is $|AB|^{2}$ , so the correct option is $\boxed{\dfrac{256}{17}}$ .

Given the answer choices, it's a simple thing to eliminate the ones that can't be, hone in on the one that must be.

Apart from that, why is it /given/ that triangles ABE and ECF are similar? Other than that they both have a right angle, you don't /know/ anything else about them? Or, you did not establish that in the "Note first that the triangles ... are similar." We know the lengths of sides of triangle AEF; that's pretty much all?

Sharon Smith - 5 years, 1 month ago

Both the triangles are right-angled, so $\angle BEA = 90^{\circ} - \angle BAE$ and $\angle CEF = 90^{\circ} - \angle CFE$ .

But $\angle BEA + 90^{\circ} + \angle CEF = 180^{\circ} \Longrightarrow \angle BEA = 90^{\circ} - \angle CEF$ as well, so $\angle BAE = \angle CEF$ , which in turn implies that $\angle BEA = \angle CFE$ . As each triangle then has the same set of interior angles we can conclude that they are similar. (They are not, however, congruent, as the side lengths differ.)

Brian Charlesworth - 5 years, 1 month ago

Exactly the same method......

Ayush Pattnayak - 5 years, 3 months ago

Damon Tabb
Mar 15, 2016

The answer choices pretty much gave this one away instantly without having to solve anything. If AE was 4, then you knew that AB would be slightly less than 4, meaning the area of the square ABCD would be "slightly less than 4" times "slightly less than 4". The only answer that worked was 256/17. Honestly, it's been too long since my geometry days, so I probably wouldn't have gotten this if I'd had to solve it the way it was done below!

I solved this the same way you did. I appreciate that people can figure out an answer--i could with enough time, but sometimes time is important. Think about timed exams and you work out a solution and then find that only one answer could be right.

Nelson Brentlinger - 5 years, 3 months ago

Ελιά Ο.Β.
Mar 23, 2016

16 would mean AB=4 which is impossible because AB is shorter than AE.

17/16 or 16/17 is way too low a number because its around One.

256 is way too high

Therefore its 256/17 which equals less than 16 and still is reasonably high enough a number.

Takes 15 seconds max to figure out ;)

I did it this way too I'm so happy I'm not the only one who didn't use a ton of calculations

Cole Cadorette - 5 years, 1 month ago

Constantin Merlusca
Apr 19, 2016

should be close to 16 but diferrent ,so no other answer except 256/17 match ;)

Kenny Galliez
Apr 19, 2016

You all say that ABE and ECF are similar triangles, and I believe you, I was about to do it that way at first too. But I just didn't because I couldnt prove this. Can you? Been a long time since geometry classes...

You can refer to a comment above by Brian for the solution. I just want to add a little bit that the two angles BAE and CEF have BA forms a right angle with CE, AE forms a right angle with CF, then they are equal angles. Excuse me for being unable to write in math. language.

Pham Minh - 5 years ago

Yves Tedera
Apr 14, 2016

Let s be the side.

From the image it could be inferred that 3 < s < 4 and area, s², is 9 < s² < 16 Among the choices, only $\frac{256}{17}$ fits this condition. Hence a quick guess.

Thomas James Bautista
Apr 2, 2016

Let $|AB| = |BC| = x$ . So, the area of the square is $x^2$

$|BE|^2+|AB|^2=|AE|^2 \Longrightarrow |BE|^2+x^2=4^2$

$\Longrightarrow |BE|=\sqrt{16-x^2}$

$|BC|=|BE|+|EC| \Longrightarrow x=\sqrt{16-x^2}+|EC|$

$\Longrightarrow |EC|=x-\sqrt{16-x^2}$

$\Delta ABE$ and $\Delta ECF$ are similar.

$\dfrac{|AB|}{|AE|}=\dfrac{|EC|}{|EF|}$

$\Longrightarrow \dfrac{x}{4}=\dfrac{x-\sqrt{16-x^2}}{3}$

$\Longrightarrow 3x=4x-4\sqrt{16-x^2}$

$\Longrightarrow x=4\sqrt{16-x^2}$

Square both sides.

$\Longrightarrow x^2=16(16-x^2)$

$\Longrightarrow x^2=256-16x^2$

$\Longrightarrow 17x^2=256$

$\Longrightarrow x^2=\boxed{\dfrac{256}{17}}$

I believe the original diagram is impossible to exist. Reason is by contradition - if we assume that the two triangles are not similar, and x is the square side length, then using only Pythagoras Theorem we can produce the following relationship on the top right triangle. That is $(x-\sqrt{16-x^2})^2+(x-\sqrt{25-x^2})^2=9$

This when solved ends up giving

$x^2 = \frac{256(41+5\sqrt{23)}}{1105}$

This produces 15.05399489 as compared to the decimal equivalent of the supposed correct answer of 15.05882353. This error is due to the initial diagram being impossible to construct as the triangles intuitively must be similar yet the solutions do not match. In future, please Mr Brilliant, can you create diagrams that exist and can be drawn in the dimensions shown.

Bruce Richard - 5 years, 1 month ago

Right Triangle Tucked Into A Square

7 solutions

0 pending reports