Triangle into 25

Geometry Level 4

Equilateral $\triangle ABC$ is divided into $25$ smaller regions by $9$ line segments, as shown.

$A', A'',$ and $A'''$ divide $\overline{AC}$ into 4 equal segments; similarly, $B', B'',$ and $B'''$ divide $\overline{BC}$ into 4 equal segments..

If the areas of the $25$ regions are all integers, what is the smallest possible area of $\triangle ABC?$

The answer is 21840.

1 solution

Jeremy Galvagni
Oct 21, 2018

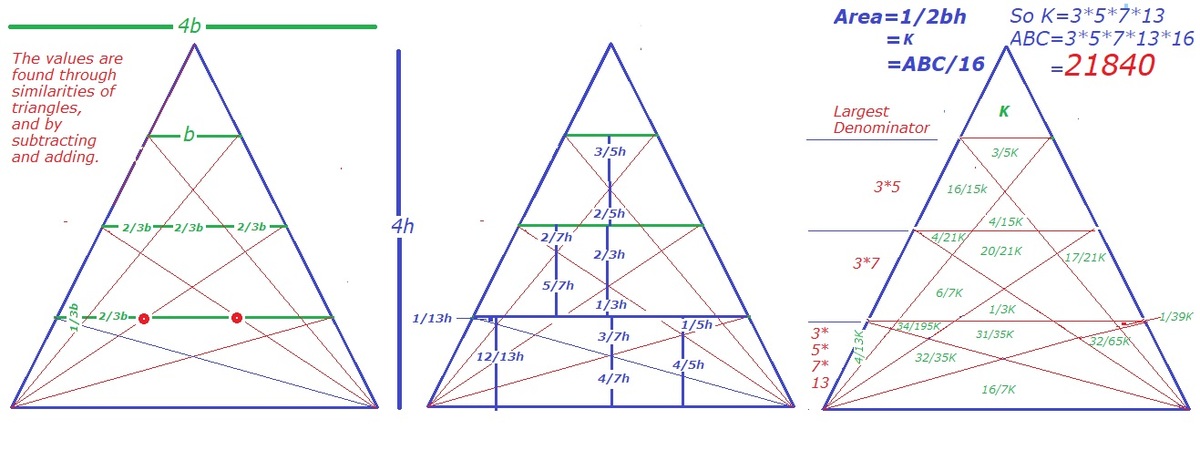
By setting the area of $\triangle A'''B'''C=1$ and using coordinate geometry, you can find the areas of the other 24 regions. These areas are all fractions whose denominators are all multiples of 3, 5, 7, and 13. The common denominator of all of them is $3 \cdot 5 \cdot 7 \cdot 13 =1365$ . Multiplying all of the areas by this factor yields:

There is no common factor to these $25$ regions. $\triangle ABC$ has $16$ times the area of $\triangle A'''B'''C$ so the final area is $1365 \cdot 16 = \boxed{21840}$

I had misunderstood the problem.
When I understood at third attempt, from my notes I copied 21845 !
In place of zero carelessly typed 5 !!

Niranjan Khanderia - 2 years, 2 months ago

Triangle into 25

The answer is 21840.

1 solution

0 pending reports