Triangles are back!
Calculate the total number of triangles in the given figure.
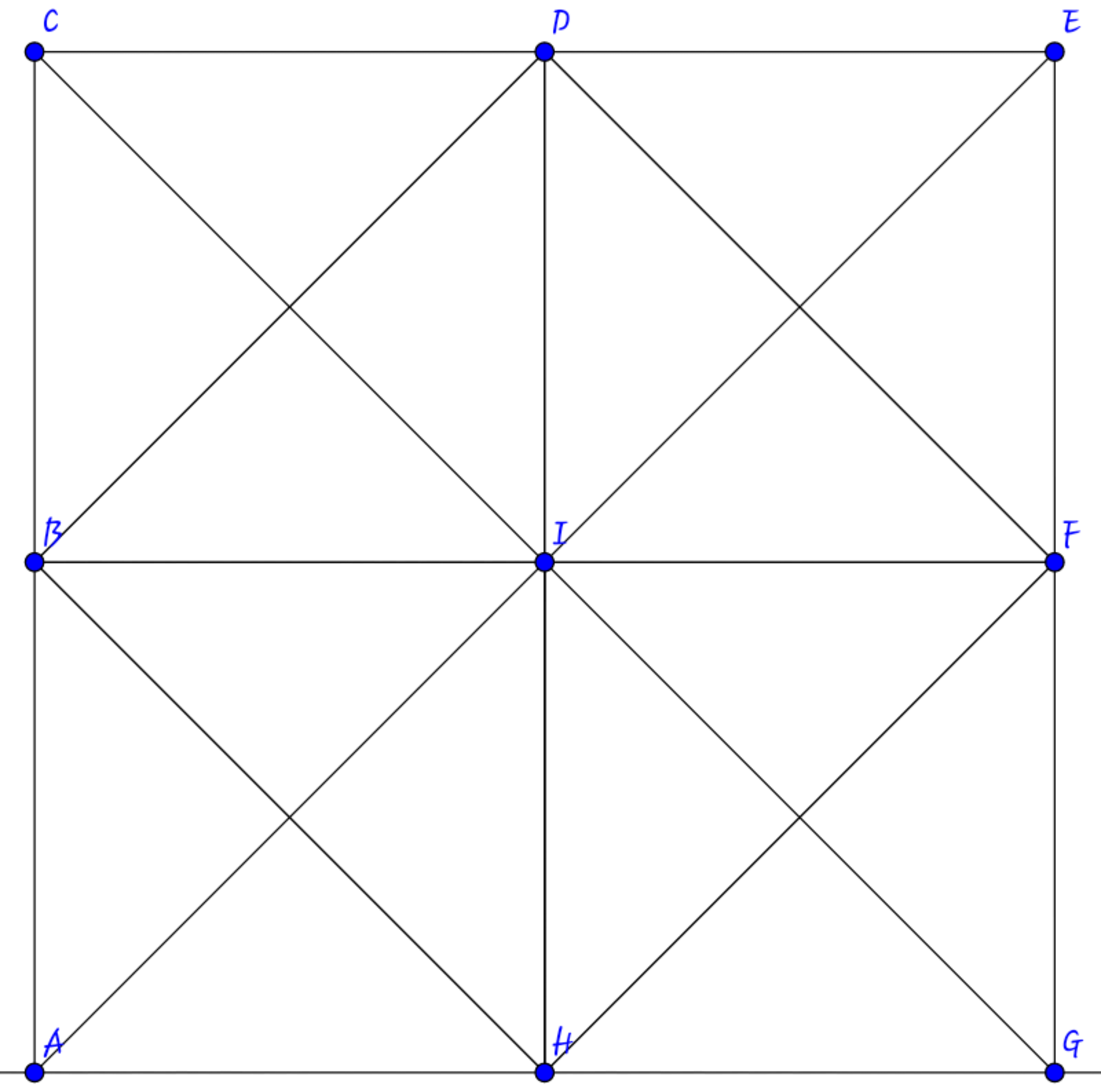
Structure:- The above figure represents a square ACEG, whose diagnols are crossed. Moreover, B, D, F and H are midpoints of AC, CE, EF and AG, respectively. Again, BDFH represents another square with its diagnols crossed.
Clarification:- I is the midpoint of the diagnols of ABCD and BDFH alike.
The answer is 44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Easy counting reveals that in □ FIDE, there are 8 triangles.
Now, □ FIDE is the same as □ FGHI, □ BAIH and □ CDBI. So, each of them have 8 triangles.
Now, forget about the lines BD, DF, FH, BH, BF and DH. Observe that □ CAGE is similar to □ FGHI. So, it too has 8 triangles.
Now, forget about the lines CE, EG, GA, AC, CG and AE. Observe that □ BDFH is similar to □ FGHI. So, it too has 8 triangles.
But in this process, we count DIF, FIH, HIB, BID twice, so they have to be subtracted, so the answer is
So, the total number of triangles in the given figure = ( ( 4 × 8 ) + 8 + 8 ) − 4 = 4 4 .