Triangle Numbers
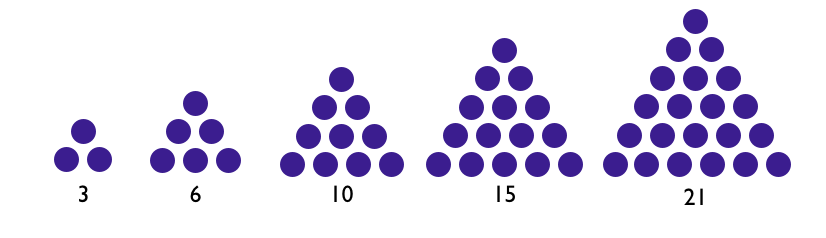
To construct the n th triangle number, start with a row of n dots. Then add a row with n − 1 dots. Continue, adding a row with one fewer dot in every step, until a row with one dot is added. The drawing above show the second through sixth triangle numbers: T 2 = 3 , T 3 = 6 , T 4 = 1 0 , T 5 = 1 5 , T 6 = 2 1 .
How much is T 9 9 + T 1 0 0 ?
Try to answer without a calculator.
Hint : Algebraic answers are great; geometric answers may be even greater!
The answer is 10000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
NIce "diamond" solution. So in general T n + T n + 1 = ( n + 1 ) 2 .
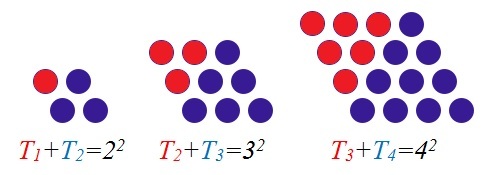
From the illustration above, it is clear that T n − 1 + T n = n 2 ⟹ T 9 9 + T 1 0 0 = 1 0 0 2 = 1 0 0 0 0 .
2 n ( n + 1 )
Use from ↑ for find T 9 9 + T 1 0 0 .
For T 9 9 we have 2 9 9 ( 9 9 + 1 = 1 0 0 ) = 4 9 5 0
For T 1 0 0 we have 2 1 0 0 ( 1 0 0 + 1 = 1 0 1 ) = 5 0 5 0
For T 9 9 + T 1 0 0 we have (4950+5050) = 10000
∴ the answer is 1 0 0 0 0
We can find a pattern here,
T2 = (2+1)C(2-1) = 3
T3 = (3+1)C(3-1) = 6
T4 = (4+1)C(4-1) = 10 ...
...
Tn = (n+1)C(n-1)
Hence, T99 + T100 = (99+1)C(99-1) + (100+1)C(100-1)
. = 100 * 99/2 + 101 * 100/2
.
. = 50 * 99 + 101 * 50
. = 50(99+101)
. = 10000
Note that (n+1)C(n-1) = (n+1)C2.
Image the triangle for T 1 0 0 , with 100 dots in the bottom row. Now take the triangle for T 9 9 , turn it upside down, and place it underneath the first triangle. The resulting figure is a diamond-- a square standing on one of its corners. Since the sides of the square contain 100 dots, the total number of dots is T 1 0 0 + T 9 9 = 1 0 0 2 = 1 0 0 0 0 .
Alternatively, it is not difficult to show that T n = 2 1 n ( n + 1 ) . We find T 1 0 0 + T 9 9 = 2 1 ⋅ 1 0 0 ⋅ 1 0 1 + 2 1 ⋅ 9 9 ⋅ 1 0 0 = 2 1 ⋅ 1 0 0 ⋅ ( 1 0 1 + 9 9 ) = 2 1 ⋅ 1 0 0 ⋅ 2 0 0 = 1 0 0 0 0 .