Triangle of 2 Arcs
One big and one small circle share the same center .
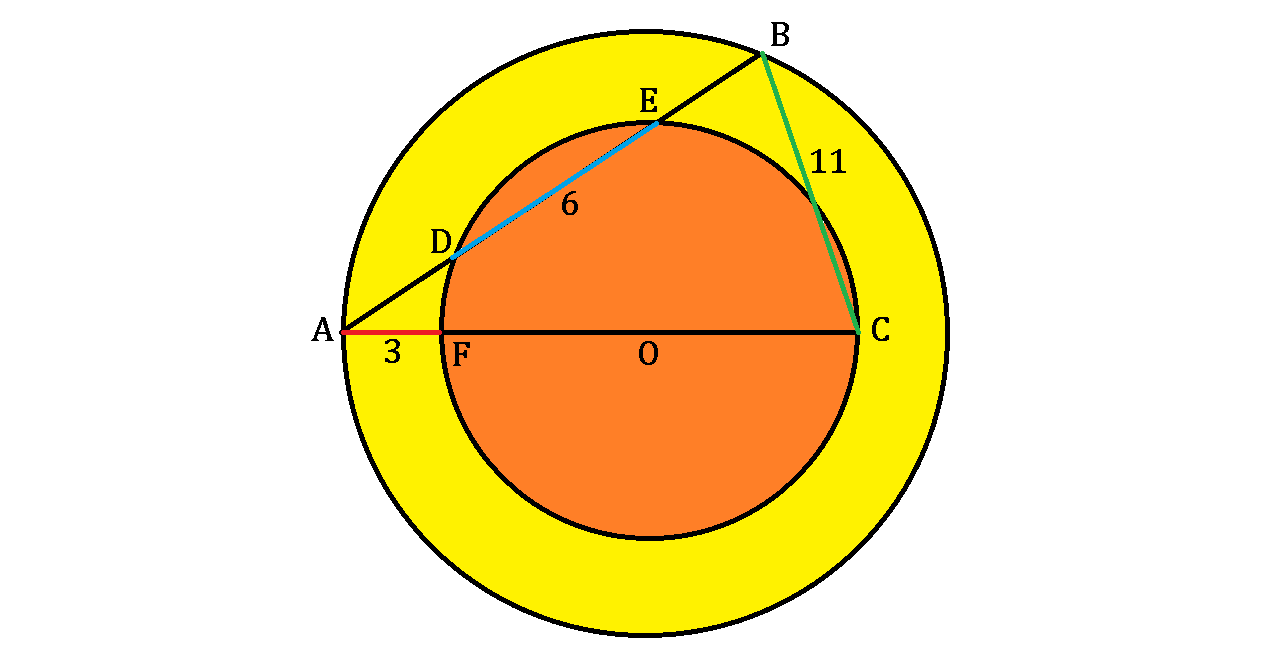
Then is constructed such that points and are on the big circle while point is on the smaller circle. intersects the smaller circle at and and passes through and , as shown above.
If (red segment), (blue segment), and (green side), what is the radius of the smaller, orange circle?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

Let point G be the midpoint of D E . Then by drawing the radii from the center O to D & E , △ O D E will be an isosceles triangle, and then O G will be the bisector of the triangle.
Let the smaller radius = r . Then by Pythagorean theorem, O D 2 = r 2 = O G 2 + D G 2 = O G 2 + 9 .
Thus, O G = r 2 − 9 .
Now consider the right △ A O G . From the image above, sin θ = A O O G = r + 3 r 2 − 9 .
Then by the Center Angle Property , ∠ B O C = 2 θ .
Hence, by Cosine Rule :
B C 2 = 1 1 2 = 1 2 1 = O B 2 + O C 2 − 2 ( O B ) ( O C ) cos 2 θ .
From the trigonometry identity, cos 2 θ = 1 − 2 sin 2 θ = 1 − ( r + 3 ) 2 2 ( r 2 − 9 )
1 2 1 = ( r + 3 ) 2 + r 2 − 2 r ( r + 3 ) + ( r + 3 ) 4 r ( r 2 − 9 ) = 9 + ( r + 3 ) 4 r ( r 2 − 9 )
1 2 1 − 9 = 1 1 2 = ( r + 3 ) 4 r ( r 2 − 9 )
2 8 ( r + 3 ) = r ( r 2 − 9 ) = r 3 − 9 r
0 = r 3 − 3 7 r − 8 4 = ( r − 7 ) ( r 2 + 7 x + 1 2 ) = ( r − 7 ) ( r + 3 ) ( r + 4 )
Thus, r = 7 .