Triangle of Intersections
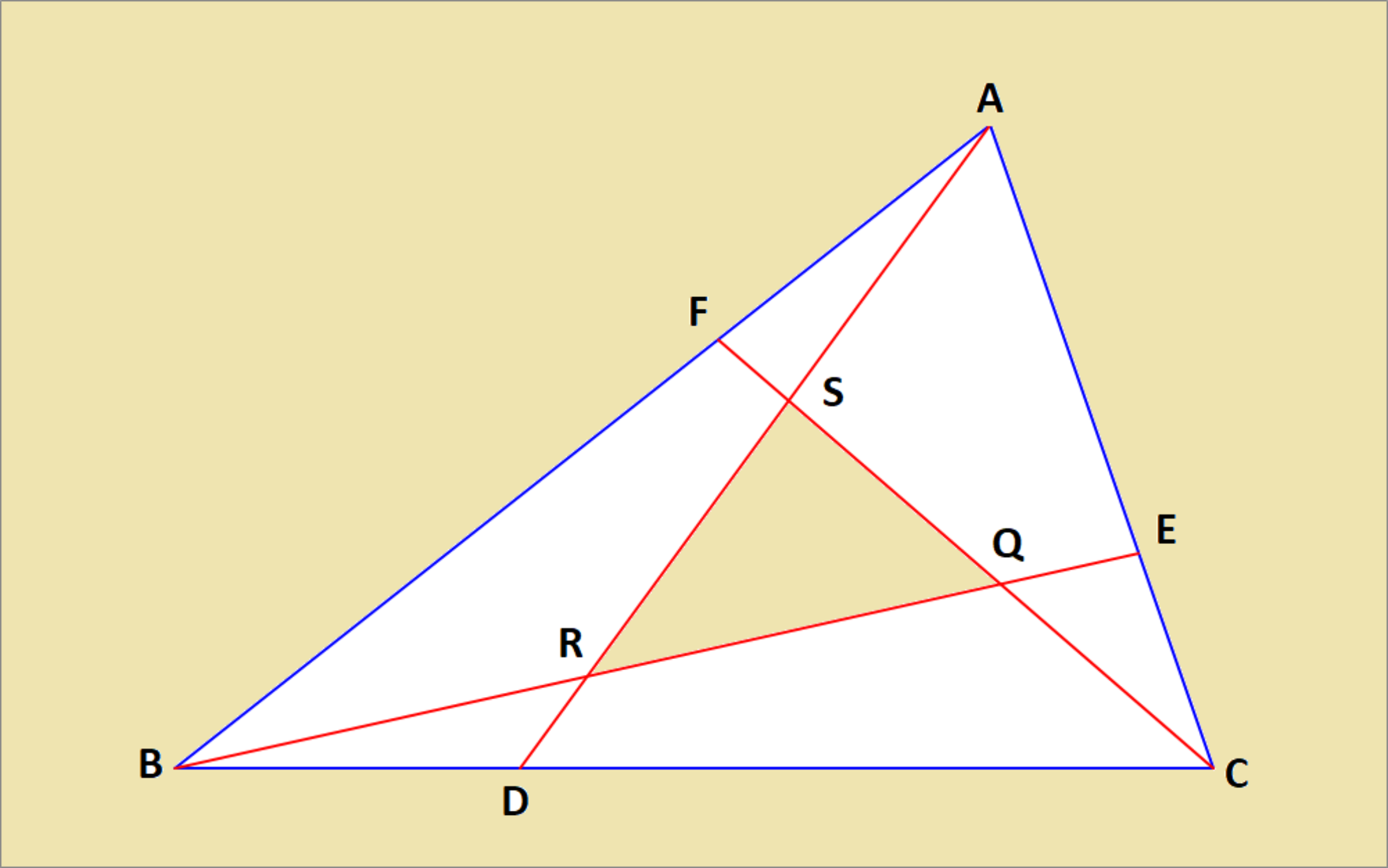
In , points , , and are on , , and are such that , where . The segments , , and intersect at three points , , and .
If the area of is half the area of , then what is the value of ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Through successive shear mappings , △ A B C can be transformed to unit equilateral triangle △ A ′ B ′ C ′ while still preserving all of its area and length ratios.
Since B C B D = A C C E = A B A F , the diagram above has rotational symmetry, so △ R ′ Q ′ S ′ is an equilateral triangle, B ′ D ′ = C ′ E ′ , and D ′ R ′ = E ′ Q ′ .
Since △ R ′ Q ′ S ′ and △ A ′ B ′ C ′ are both equilateral triangles, and since △ R Q S is half the area of △ A B C , and since the sides of △ A ′ B ′ C ′ are 1 , the sides of △ R ′ Q ′ S ′ must be 2 2 .
Also since △ R ′ Q ′ S ′ and △ A ′ B ′ C ′ are both equilateral triangles, ∠ A ′ C ′ B ′ = 6 0 ° and ∠ Q ′ R ′ S ′ = 6 0 ° , and by vertical angles ∠ B ′ R ′ D ′ = 6 0 ° as well. This means that △ B ′ R ′ D ′ ∼ △ B ′ C ′ E ′ by AA similarity, so B ′ R ′ D ′ R ′ = B ′ C ′ C ′ E ′ and B ′ R ′ B ′ D ′ = B ′ C ′ B ′ E ′ . Substituting C ′ E ′ = B ′ D ′ , B ′ C ′ = 1 , and B ′ E ′ = B ′ R ′ + 2 2 + D ′ R ′ gives B ′ R ′ D ′ R ′ = B ′ D ′ and B ′ R ′ B ′ D ′ = B ′ R ′ + 2 2 + D ′ R ′ . Furthermore, using the law of the cosines on △ B ′ R ′ D gives B ′ D ′ 2 = B ′ R ′ 2 + D ′ R ′ 2 − B ′ R ′ ⋅ D ′ R ′ .
These three equations solve to B ′ D ′ = α = 4 2 2 1 − 3 2 1 ≈ 0 . 1 7 3 .