Triangle of Reflection

Geometry Level 3

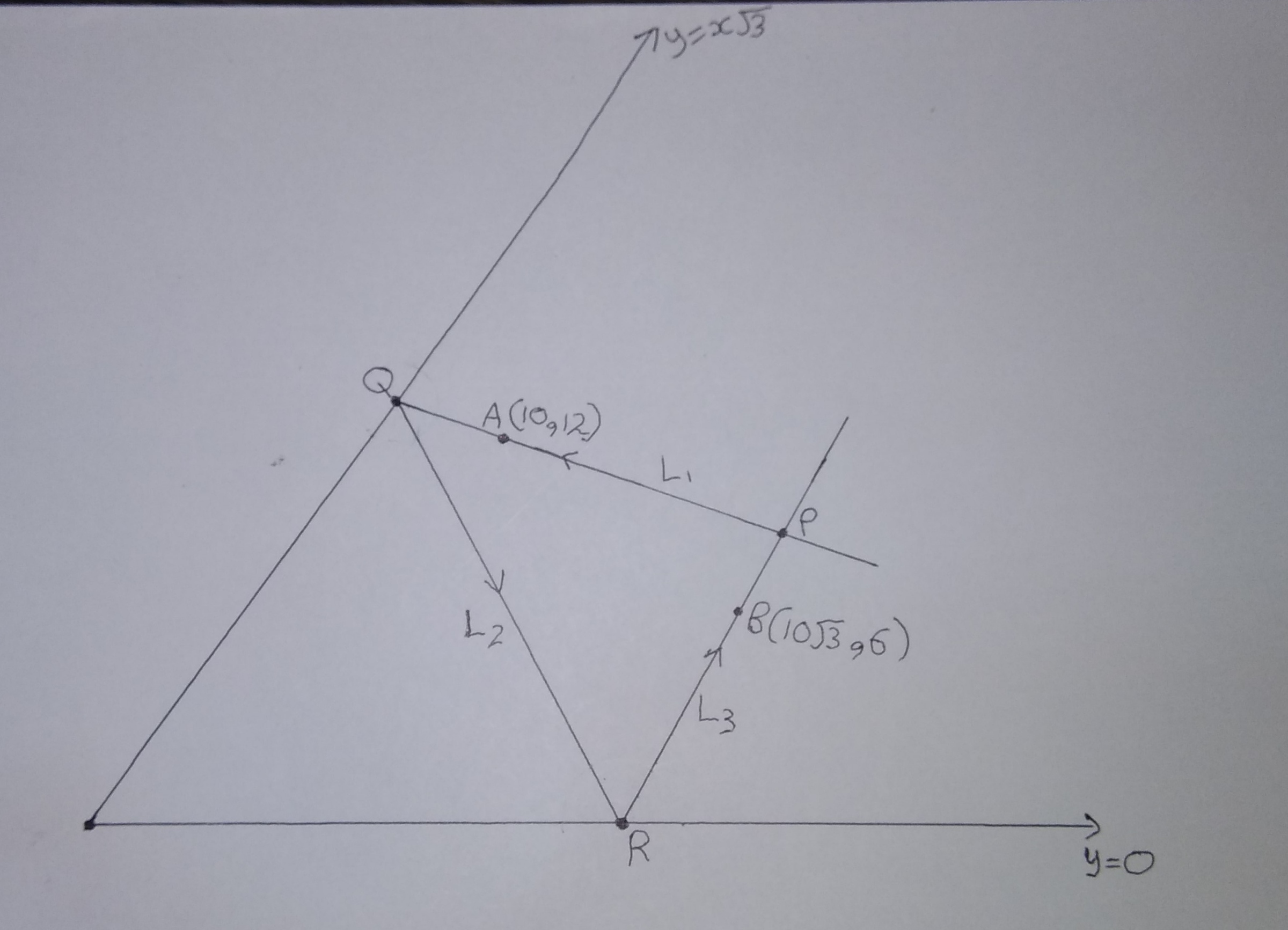
Passing through a point $A(10, 12)$ , a line $L_1$ is incident on $y = x\sqrt3$ at point $Q(x_1, y_1)$ . The reflected ray $L_2$ is incident on $y = 0$ at point $R(x_2, y_2)$ . The now reflected ray $L_3$ passes through point $B(10\sqrt3, 6)$ . Lines $L_1$ and $L_3$ meet at point $P(x_3 , y_3)$ .

Find area of $\Delta PQR$ . If area is of form $a\sqrt{b} \text{ where } a, b\in \N \text{ and } b \text{ is squarefree}$ , enter answer as $a + b$ .

All of my problems are original

The answer is 51.

1 solution

Aryan Sanghi
Sep 8, 2020

Let image of $A(10, 12)$ on $y = x\sqrt3$ be $A'$ and $B(10\sqrt3, 6)$ on $y = 0$ be $B'$

Image of point $(h, k)$ on line $ax + by + c = 0$ is $(x, y)$ and is found using

$\frac{x - h}{a} = \frac{y - k}{b} = -2\frac{ah + bk + c}{a^2 + b^2}$

Applying above formula, we get

$A' \equiv (6\sqrt3 - 5, 5\sqrt3 + 6) \text{ and } B' \equiv (10\sqrt3, -6)$

Now, as $A', Q, R, B'$ are collinear, $\text{equation of } A'B' = \text{equation of }QR$

$L_2 = A'B'$ $L_2 = \sqrt3x + y - 24 = 0$

So, solving $L_2$ with mirrors, we get

$\boxed{Q \equiv (4\sqrt3, 12) \text{ and } R \equiv (8\sqrt3, 0)}$

Now,

$L_1 = AQ \text{ and } L_2 = BR$ $L_1 = y - 12 = 0 \text{ and } L_2 = \sqrt3x - y - 24 = 0$

Solving $L_1$ and $L_2$ , we get

$\boxed{P \equiv (12\sqrt3, 12)}$

Therefore,

$\color{#3D99F6}{\boxed{\text{ar}(\Delta PQR) = 48\sqrt3}}$

So, $a = 48, b = 3, a + b = 51$

Wonderful method。

A Former Brilliant Member - 9 months ago

Thanku. :)

Aryan Sanghi - 9 months ago

Triangle of Reflection

The answer is 51.

1 solution

0 pending reports