Triangle of Tangency

Calculus Level pending

[ Background Information ]

The equation for the yellow curve is: $1+sin(x)$

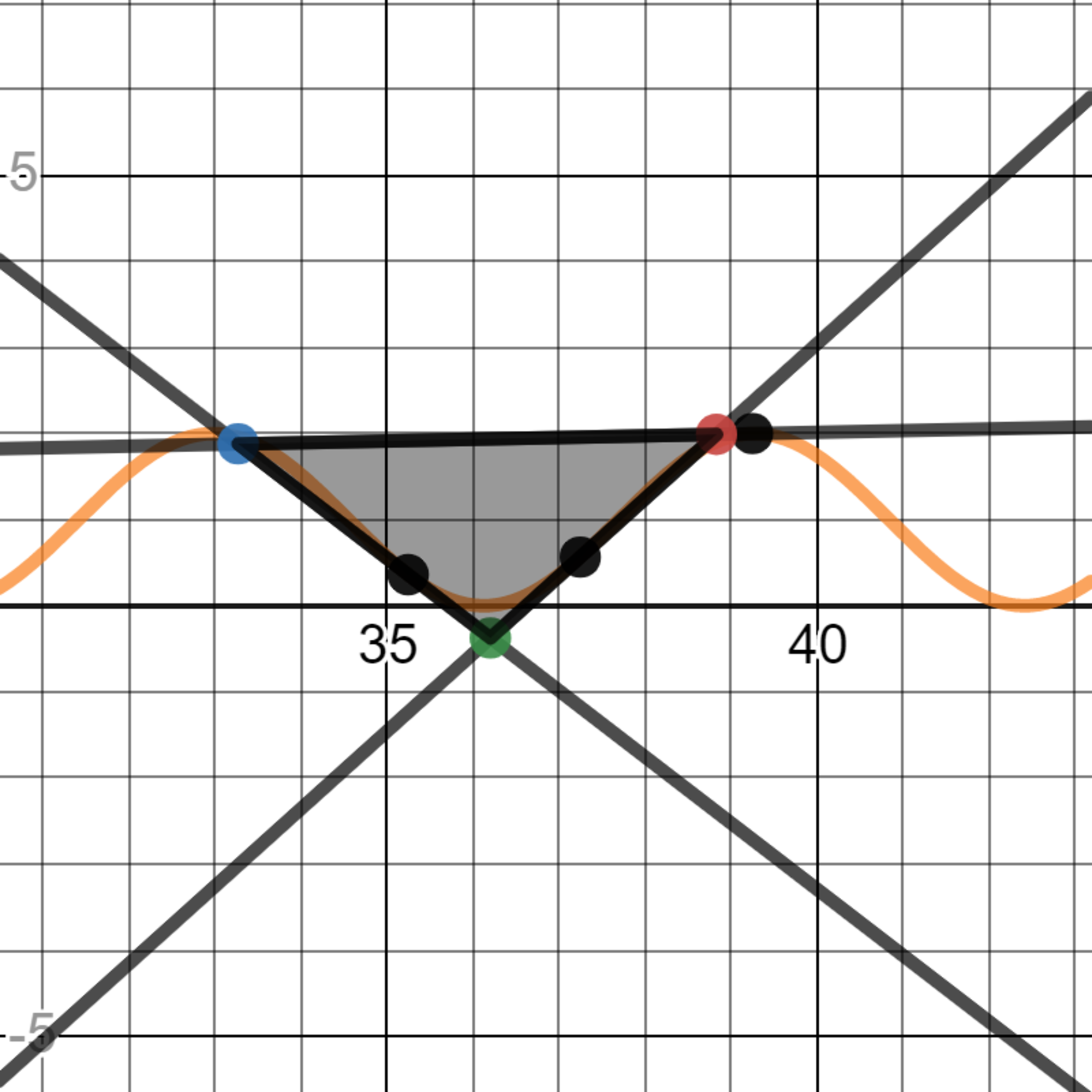
The three black points have lines that are TANGENT to f(x) going through them.

The three tangent lines form a triangle with three colored intersections (The Blue Point, Green Point, and the Red Point).

The coordinates of the three black dots are:

-The leftmost point : (a,f(a))

-The middle point: (a+2,f(a+2))

-The rightmost point: (a+4,f(a+4))

A(x) is the area of the triangle created by the three colored intersections (The Blue Point, Green Point, and the Red Point).

[ Question ]

What is the instantaneous change of A(x) when a = 32.25? Then nest the answer in the triangle area function.

[ Answer Submission ]

What is A(32.25)?

Pick the answer that is closest to ( A(32.25) - 9.396 )!

[ Additional Information ]

If there is something wrong with the problem(ex. Problem is not explained properly; Answer is incorrect; etc), don't hesitate to DM me on brilliant.

0.738 1.337 1.715 0.515 0.395

1 solution

S. P.
Jan 20, 2020

[ Declare Functions ]

f(x) = 1+sin(x)

f'(x)=cos(x)

[ Tangent Lines to the Three Points ]

$l_{1}\left(x\right)=f'\left(a\right)x+\left(-f'\left(a\right)*a+f\left(a\right)\right)$

$l_{2}\left(x\right)=f'\left(a+2\right)x+\left(-f'\left(a+2\right)*(a+2)+f\left(a+2\right)\right)$

$l_{3}\left(x\right)=f'\left(a+4\right)x+\left(-f'\left(a+4\right)*(a+4)+f\left(a+4\right)\right)$

[ Use of Linear Algebra to find Intersections of the Tangent Lines ]

Point A: [ $\frac{\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)-\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a+2\right)}$ , $\frac{f'\left(a+4\right)\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)-f'\left(a+2\right)\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a+2\right)}$ ]

Point B: [ $\frac{\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a\right)}$ , $\frac{f'\left(a+4\right)\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-f'\left(a\right)\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a\right)}$ ]

Point C: [ $\frac{\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)}{f'\left(a+2\right)-f'\left(a\right)}$ , $\frac{f'\left(a+2\right)\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-f'\left(a\right)\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)}{f'\left(a+2\right)-f'\left(a\right)}$ ]

[ Using Distance Formula to Calculate Side Lengths ]

$s_{1}=\sqrt{\left(\frac{\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)-\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a+2\right)}-\frac{\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a\right)}\right)^{2}+\left(\frac{f'\left(a+4\right)\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)-f'\left(a+2\right)\left(-f'\left(a+4\right)c+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a+2\right)}-\frac{f'\left(a+4\right)\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-f'\left(a\right)\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a\right)}\right)^{2}}$

$s_{2}=\sqrt{\left(\frac{\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a\right)}-\frac{\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)}{f'\left(a+2\right)-f'\left(a\right)}\right)^{2}+\left(\frac{f'\left(a+4\right)\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-f'\left(a\right)\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a\right)}-\frac{f'\left(a+2\right)\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-f'\left(a\right)\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)}{f'\left(a+2\right)-f'\left(a\right)}\right)^{2}}$

$s_{3}=\sqrt{\left(\frac{\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)-\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a+2\right)}-\frac{\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)}{f'\left(a+2\right)-f'\left(a\right)}\right)^{2}+\left(\frac{f'\left(a+4\right)\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)-f'\left(a+2\right)\left(-f'\left(a+4\right)\cdot\left(a+4\right)+f\left(a+4\right)\right)}{f'\left(a+4\right)-f'\left(a+2\right)}-\frac{f'\left(a+2\right)\left(-f'\left(a\right)\cdot a+f\left(a\right)\right)-f'\left(a\right)\left(-f'\left(a+2\right)\cdot\left(a+2\right)+f\left(a+2\right)\right)}{f'\left(a+2\right)-f'\left(a\right)}\right)^{2}}$

[ Heron's Formula to find area. ]

$p=\frac{s_{1}+s_{2}+s_{3}}{2}$

A(x) = $\sqrt{p\left(p-s_{1}\right)\left(p-s_{2}\right)\left(p-s_{3}\right)}$

A(32.25) = 10.134

10.134 - 9.396 = 0.738

Triangle of Tangency

1 solution

0 pending reports