Triangle pattern
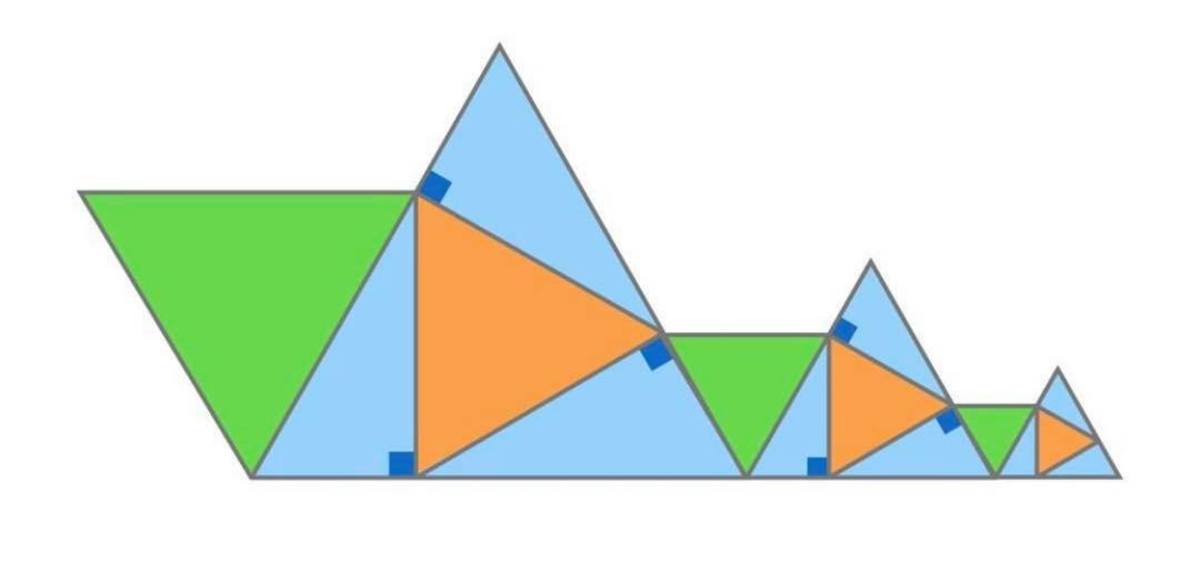
In the image above, the green, blue, and orange triangles are all equilateral triangles. How many times is the area the leftmost green triangle of that of the rightmost orange triangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To start you can see the green triangles are getting their height cut in half, and height is proportional to side length so the side length will also be cut in half. Therefor in total you will be cutting the area in 4. Therefore green to green to green divides the area into 16. It is obvious that orange is smaller than green so that eliminates 9 and 27/2 as possible answers, since they are both less than 16.
So to find the answer we just need to find the first green to orange ratio and multiply that by 16.
I just set side length of first green to equal 10, which makes the height 5 3 and an area of 25 3 . The side length for the first orange is also 5 3 (same as the height for green). Using the height formula for equilateral triangles, that gives a height for orange of 7.5 units. Applying the area formula to that gives 18.75 3 for orange's area. The ratio of 25 3 to 18.75 3 is 4/3.
Therefore the ratio for biggest green to smallest orange is 4/3 time 16 or 64/3