Triangle in circle

Let $O$ be the centre of the circle/triangle, and let $r$ be the radius of the circumcircle. Consider $\triangle OAB$ , $\triangle OBC$ or $\triangle OCA$ :

$\frac{6}{sin120}=\frac{r}{sin30}$ $r=\frac{6\times \frac{1}{2}}{\frac{\sqrt{3}}{2}}=2\sqrt{3}$

The area of a circle is $\pi{r}^{2}$ , therefore $k={r}^{2}=4\times 3 = \color{#20A900}{\large \boxed{12}}$

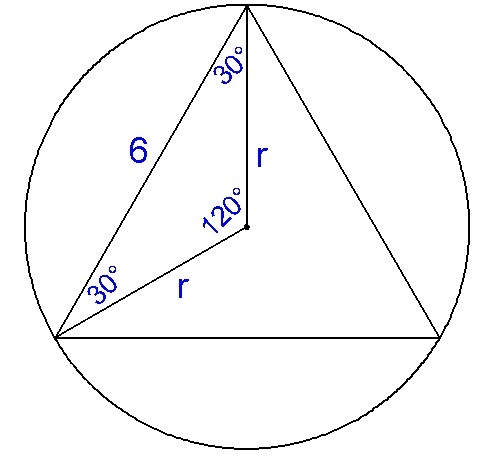By cosine law,

$6^2=r^2+r^2-2(r)(r) \cos 120$

$36=2r^2-2r^2 \cos 120$

$r^2=12$

The area of a circle is given by the formula: $A=\pi r^2$ where $r$ is the radius. It follows that $k=r^2$ .

So,

$\boxed{k=12}$

Center of the circle = Centroid of the triangle...

altitude of Eq. triangle = sqrt(3) / 2 * side of the triangle...

Centroid divides each of the medians in the ratio 2:1...

Hence radius of the circumcircle will be (2/3) * altitude of Eq. triangle => (2/3) * sqrt(3) / 2 * side of the triangle

=> r = (2/3) * (sqrt(3) / 2 * 6) = 2 * sqrt(3)

Here k = r * r

k = 4 * 3 = 12.

This is the easiest method to solve this thing, albeit a bit long. 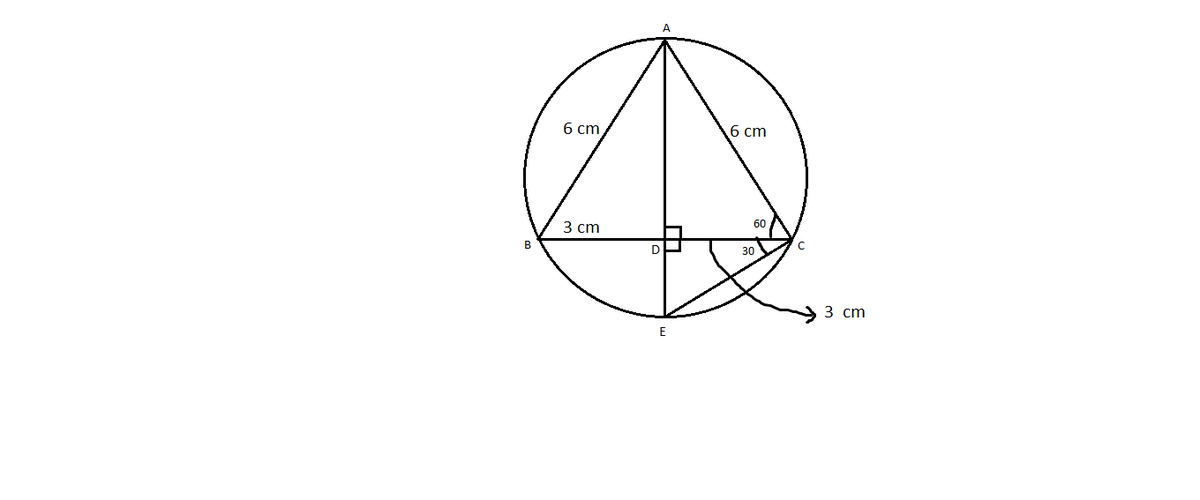So, we know that the median of an equilateral triangle passes through the center of a circle, it is also the perpendicular bisector of the side it falls on(the side in our case is BC). So we construct chord AE, which is the diameter as it is passing through the center. Therefore, AE divides our circle into 2 semi-circles. This implies, - Angle ADC = Angle EDC = 90 Now, - Angle ACE = 90(Since angle in a semicircle is 90)----------------------(Equation 1) - Angle ACD = 60(Since triangle ABC is equilateral)---------------------(Eq. 2) From Eq(1) and (2), Angle ECD = 30(Angle ACE - Angle ACD) Now applying trigonometric values, - cot30 = \sqrt{3} = $\frac{3}{DE}$ Therefore, - DE = $\frac{3}{\sqrt{3}}$ = \sqrt{3} Now,
- cosec 60 = $\frac{3}{AD}$ = $\frac{2}{\sqrt{3}}$ Hence, - AD = 3\sqrt{3} Now, diameter = AE = AD + DE = \sqrt{3}+3\sqrt{3} = 4\sqrt{3} Area of Circle = πr^{2} = π x $\frac{AE}{2}$ ^{2} = kπ cm^{2} Therfore, - π x $\frac{AE^{2}}{4}$ = π x $\frac{48}{4}$ = 12π = kπ On comparing LHS and RHS, - k = 12 Hence, k = 12

Using Extended Sine Rule, we have that

$\dfrac{6}{\sin (60^{\circ})} = 2R$

where $R$ represents the circumradius. Solving the above equation, we have

$\dfrac {3}{\frac{\sqrt{3}}{2}} = R$

$R = \dfrac {6}{\sqrt{3}}$

The area of the circumcircle is

$\pi \times R^2 = \pi \times \dfrac {36}{3} = 12\pi$

Therefore, $k = 12$ .

Form sine formula...... (6/sin60°)=2R................... We know the area of the circle......πR^2=12π.......... Here angle is 60° .because it is an equal sides triangle.