Triangle product puzzle
In this puzzle, number written on every triangle equals the product of numbers written on three bottom triangle. Also every number must be a positive Integer greater than 1.
And A + B = 4 5 ,
You need to find the value of 2 5 C A − 1 B − 2 .
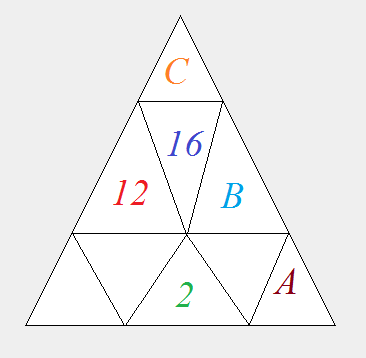
Example for how this puzzle works is given here:
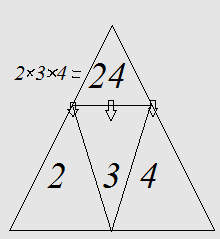
For the triangle with vertex at bottom, it works as follows:
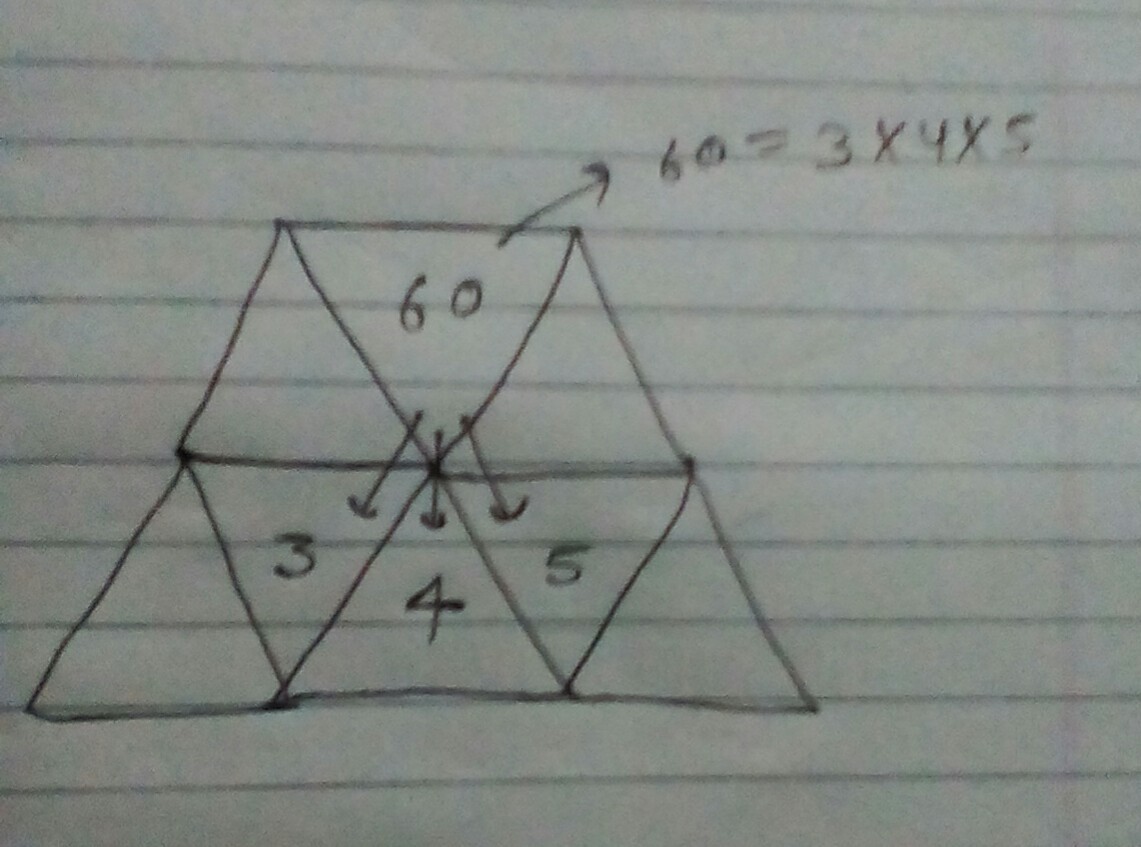
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 We have
8
B
=
A
⟹
A
+
B
=
4
5
⟹
9
B
=
4
5
⟹
B
=
5
We have
8
B
=
A
⟹
A
+
B
=
4
5
⟹
9
B
=
4
5
⟹
B
=
5
Then A = 4 5 − 5 = 4 0 ⟹ C = 1 2 × 1 6 × 5 = 9 6 0
The answer is 4 0 9 6 0 = 2 4 .
I think the letters A and B must be switched in the equations.
B is the product of three triangles below it, so B = 2 * 4 * A = 8A. B = 8A is correct and A = 8B is not.
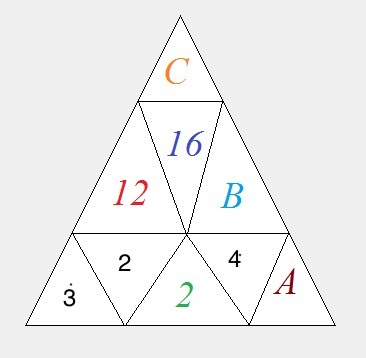
Label the missing triangles D , E , and F , as shown below:
Then 2 E D = 1 2 and 2 E F = 1 6 , which simplifies to E D = 6 and E F = 8 . Since every number is a positive integer greater than 1 , E must be a factor of 6 and 8 and greater than 1 , which means E = 2 . Since E D = 6 and E F = 8 and E = 2 , D = 3 and F = 4 .
We also know that 2 A F = B , and since F = 4 , B = 8 A . We are given that A + B = 4 5 , and substituting B = 8 A gives 9 A = 4 5 , which means A = 5 . Since A = 5 and B = 8 A , B = 4 0 .
Since C = 1 2 ⋅ 1 6 ⋅ B and B = 4 0 , C = 7 6 8 0 .
Therefore, 2 5 C A − 1 B − 2 = 2 5 ⋅ 7 6 8 0 ⋅ 5 − 1 ⋅ 4 0 − 2 = 2 4 .