Triangle Riddle

The height ratio of the red and the blue triangles is 1 :2. Let the green area is x. Then by similarity concept , 9/(29+x) = (1/2)^2, then x= 7

From Trapezoid Riddle , we have learnt that the intersection point of the trapezoid's diagonals will be the midpoint of the parallel line passing through it. That means each red triangle will have the same base length and height, so they will have the same area. Since the blue triangle has the same base and the same area as $2$ red ones, that means the blue triangle's height is twice that of the red.

Suppose the topmost & shortest line's length be $a$ and the big triangle's base length be $b$ . According to Crossed Ladders Theorem the middle parallel line's length equals $c=\dfrac{2ab}{a+b}$ . The height of the yellow small triangle will then equal $h_{1} = \dfrac{18}{a}$ because $9 = \dfrac{1}{2}\cdot a \cdot \dfrac{18}{a}$ .

Let $h_{2}$ be the height of the medium triangle. Then by similarity, $\dfrac{h_{2}}{h_{1}} = \dfrac{c}{a}$ . Thus, $h_{2} = h_{1}\cdot \dfrac{c}{a}$ . Hence, the height of the green trapezoid = $h_{2}-h_{1} = h_{1}\cdot (\dfrac{c}{a}-1) = h_{1}\cdot (\dfrac{2b}{a+b} - 1) = h_{1}\cdot (\dfrac{b-a}{a+b})$

Then let $h_{2}$ be the height of the big triangle. Then by similarity, $\dfrac{h_{3}}{h_{1}} = \dfrac{b}{a}$ . Thus, $h_{3} = h_{1}\cdot \dfrac{b}{a}$ .

Hence, the height of the orange trapezoid = $h_{3}-h_{2} = h_{1}\cdot (\dfrac{b}{a}-\dfrac{c}{a}) =h_{1}\cdot (\dfrac{b}{a})(1- \dfrac{c}{b}) = h_{1}\cdot (\dfrac{b}{a})(1-\dfrac{2a}{a+b}) = h_{1}\cdot (\dfrac{b}{a})(\dfrac{b-a}{a+b})$ .

That means the ratio of the height of the orange to green trapezoid equals $\dfrac{b}{a}$ , and with the twice height of blue to red triangle, that means $\dfrac{b}{a} = 2$ .

By similarity, the ratio of the area will be times by $2^2 = 4$ . Thus, the total area of the big triangle = $4\times 9 = 36$ .

Finally, the green trapezoid's area = $36 - 20 -9 = \boxed{7}$ .

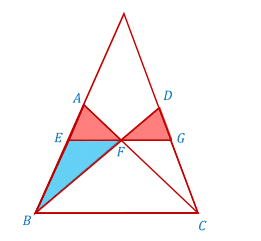
The bases of the two red triangles have the same size.

This follows from the fact that $\triangle AEF$ is similar to $\triangle ABC$ and $\triangle DFG$ is similar to $\triangle DBC$ , both with the same ratios of sides since both red triangles have the same height as do the triangles they are similar to. The two large triangles share a base, $AB$ , so the bases of the red triangles are equal to each other.

Height of green band is half the height of the tan band.

Blue triangle $BEF$ and red triangle $AEF$ share a base, so if the area of the blue triangle is equal to that of both red ones, it has to be twice that of a single red one, and that means the height of the blue one has to be twice the height of the red one.

We can set $Height_{Yellow}=\frac{1}{2}\times Base_{Yellow}=3$

Since we are only given areas, we will not be able to resolve the individual contributions height and base make to those numbers. The flip side of that is that we can set the ratio of the two to anything convenient without the choice influencing the final outcome.

Let’s define $x=Height_{Green}$

$Height_{Green+Yellow}=\frac{1}{2}\times Base_{Green+Yellow}=3+x$

$Area_{Green+Yellow}=(3+x)^2$

$Area_{Orange+Green+Yellow}=(3+3x)^2$

$Area_{Orange+Green+Yellow}-Area_{ Green+Yellow}=20$

$(3+3x)^2-(3+x)^2=20$

There is only one positive solution to this equation, and it is $x=1$

So the area of the green band is $Area_{Green}=Area_{Green+Yellow}-9=(3+1)^2-9=\boxed{7}$