Triangle side

Relevant wiki: Pythagorean Theorem

Let the triangle be $\triangle ABC$ with altitude $AE =h$ , the unknown side $AD=x$ and $CE=a$ . Then by Pythagorean theorem,

$\begin{cases} h^2 + a^2 = 8^2 & ...(1) \\ h^2 + (6-a)^2 = 7^2 & ...(2) \\ h^2 + (a-2)^2 = x^2 & ...(3) \end{cases}$

From $(2)$ :

$\begin{aligned} {\color{#3D99F6}h^2 + a^2} - 12a+36 & = 7^2 & \small \color{#3D99F6} \text{Note }(1): h^2+a^2 = 8^2 \\ {\color{#3D99F6}64} - 12a+36 & = 49 \\ \implies a & = \frac {17}4 \end{aligned}$

From $(5)$ :

$\begin{aligned} x^2 & = {\color{#3D99F6}h^2+a^2} - 4{\color{#D61F06}a} + 4 & \small \color{#D61F06} \text{Note }(2): a = \frac {17}4 \\ & = {\color{#3D99F6}64} - 4\times {\color{#D61F06}\frac {17}4} + 4 \\ & = 51 \implies x & = \sqrt{51} \approx \boxed{7.141} \end{aligned}$

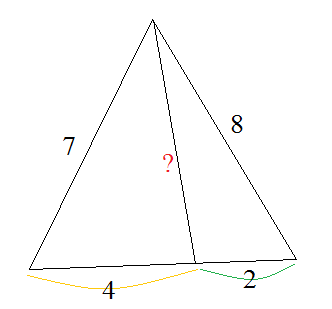
Same as Brian Charlesworth and Edwin Gray. Equating Cos of bottom left angle due to triangles 7-4-? and 7-6-8,
$\dfrac{49+16-?^2}{2*7*4}=\dfrac{49+36-64}{2*7*6}\\ \implies~\dfrac{65-?^2}{2}=\dfrac{21}{3}\\ \therefore~?=\sqrt{51}=7.141428.$ $LaTeX$

Calculate cos(A), (<A opposite side = 8) by law of cosines. 64 = 36 + 49 - 2 7 6 cos(A) gives cos(A) = 1/4. Now repeat with the desired length being calculated: y^2 = 49 + 16 - 2 7 4 .25 = 51, so y = sqrt(51) = 7.141. Ed Gray

Let the lower left angle of the given triangle be $\theta$ . Then by the cosine rule used on the full triangle we find that

$8^{2} = 6^{2} + 7^{2} - 2 \times 6 \times 7 \times \cos(\theta) \Longrightarrow 84 \cos(\theta) = 36 + 49 - 64 = 21 \Longrightarrow \cos(\theta) = \dfrac{1}{4}$ .

Next, letting the sought after side length be $x$ and using the cosine rule on the triangle with side lengths $4,7,x$ we find that

$x^{2} = 4^{2} + 7^{2} - 2 \times 4 \times 7 \times \cos(\theta) \Longrightarrow x^{2} = 65 - 56 \times \dfrac{1}{4} = 65 - 14 = 51 \Longrightarrow x = \boxed{\sqrt{51}}$ .

A simple application of Stewart's theorem........