Triangle Swivel
The large triangle in the diagram below is equilateral.
The following formula gives the area of the small triangle at the center as a fraction of the area of the large triangle: Area of large triangle Area of small triangle = α cos 2 ( θ + β π ) , where α and β are positive integers. Find α + β .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How did you know that when θ= π/6 the area of the small triangle is 0 , and when θ=0 the area of the small triangle =the area of the big triangle? I know that if we write the opposite , we will not find the correct ratio , but why can't we say that when θ=0 the area of the small triangle = 0 ??
Log in to reply
Knowing that the angles of an equilateral triangle are each 60°, we can find the other angles easily:
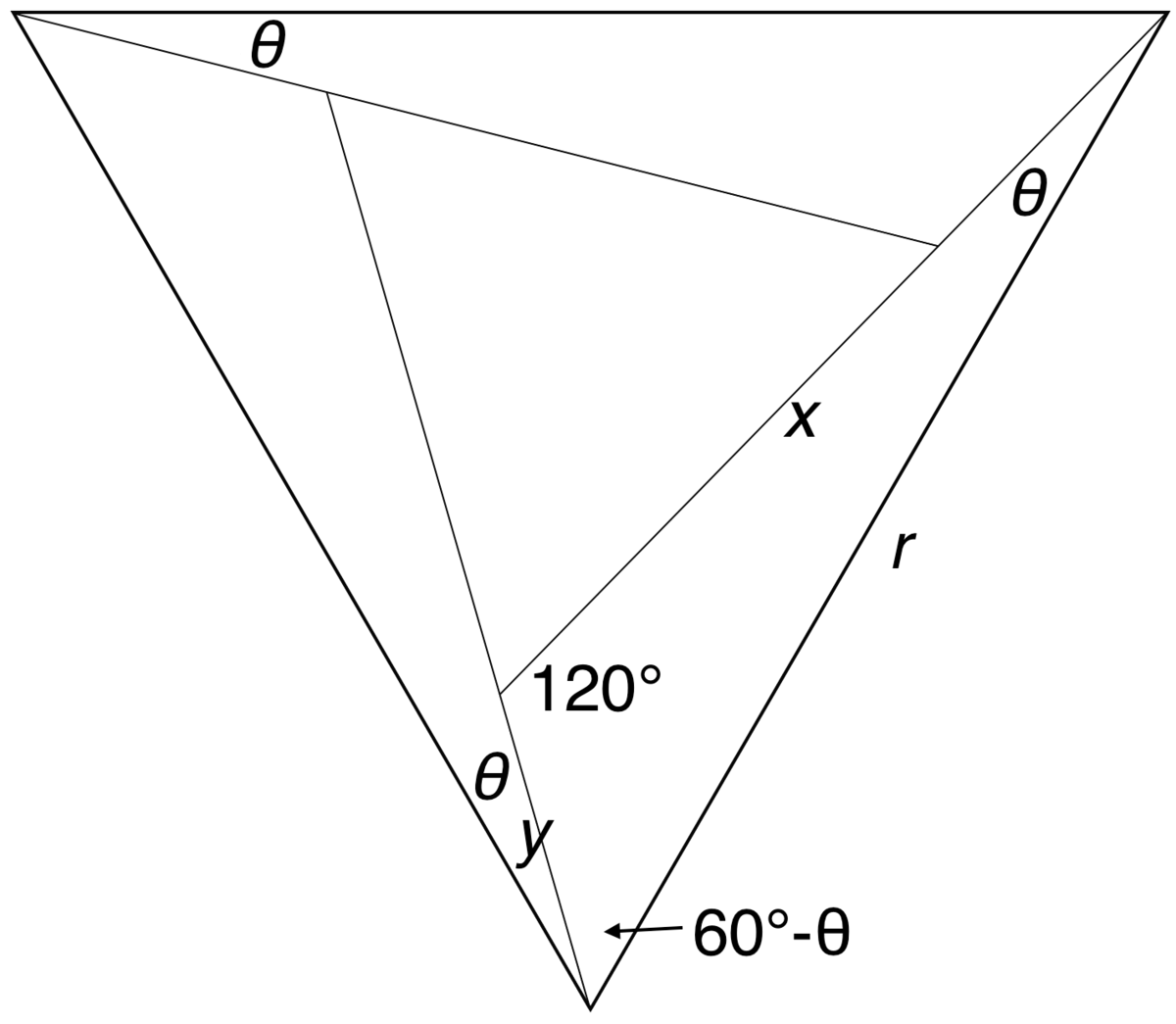 Now we can use the sin rule to get the side lengths x and y in terms of r and theta:
s
i
n
A
a
=
s
i
n
B
b
sin
A
a
sin
(
6
0
∘
−
θ
)
x
x
x
x
=
sin
B
b
=
sin
(
1
2
0
∘
)
r
=
3
2
r
sin
(
6
0
∘
−
θ
)
=
3
2
r
(
sin
6
0
∘
cos
θ
−
cos
6
0
∘
sin
θ
)
=
3
r
(
3
cos
θ
−
sin
θ
)
sin
A
a
sin
(
θ
)
y
y
=
sin
B
b
=
sin
(
1
2
0
∘
)
r
=
3
2
r
sin
(
θ
)
The side length of the small triangle is:
x
−
y
=
3
r
(
3
cos
θ
−
3
sin
θ
)
=
r
(
cos
θ
−
3
sin
θ
)
Now is a good time to use auxiliary angle method to reduce it to:
x
−
y
=
2
r
cos
(
θ
+
3
π
)
And finally, we use the formula for the area of a triangle:
A
r
e
a
o
f
a
t
r
i
a
n
g
l
e
=
2
1
a
b
sin
C
A
r
e
a
o
f
s
m
a
l
l
t
r
i
a
n
g
l
e
=
2
1
(
2
r
cos
(
θ
+
3
π
)
)
2
sin
6
0
∘
=
3
r
2
cos
2
(
θ
+
3
π
)
A
r
e
a
o
f
b
i
g
t
r
i
a
n
g
l
e
=
2
1
r
2
sin
6
0
∘
=
4
3
r
2
A
r
e
a
o
f
b
i
g
t
r
i
a
n
g
l
e
A
r
e
a
o
f
s
m
a
l
l
t
r
i
a
n
g
l
e
=
4
3
r
2
3
r
2
cos
2
(
θ
+
3
π
)
=
4
cos
2
(
θ
+
3
π
)
So
α
=
4
and
β
=
3
, so the answer is 7.
Now we can use the sin rule to get the side lengths x and y in terms of r and theta:
s
i
n
A
a
=
s
i
n
B
b
sin
A
a
sin
(
6
0
∘
−
θ
)
x
x
x
x
=
sin
B
b
=
sin
(
1
2
0
∘
)
r
=
3
2
r
sin
(
6
0
∘
−
θ
)
=
3
2
r
(
sin
6
0
∘
cos
θ
−
cos
6
0
∘
sin
θ
)
=
3
r
(
3
cos
θ
−
sin
θ
)
sin
A
a
sin
(
θ
)
y
y
=
sin
B
b
=
sin
(
1
2
0
∘
)
r
=
3
2
r
sin
(
θ
)
The side length of the small triangle is:
x
−
y
=
3
r
(
3
cos
θ
−
3
sin
θ
)
=
r
(
cos
θ
−
3
sin
θ
)
Now is a good time to use auxiliary angle method to reduce it to:
x
−
y
=
2
r
cos
(
θ
+
3
π
)
And finally, we use the formula for the area of a triangle:
A
r
e
a
o
f
a
t
r
i
a
n
g
l
e
=
2
1
a
b
sin
C
A
r
e
a
o
f
s
m
a
l
l
t
r
i
a
n
g
l
e
=
2
1
(
2
r
cos
(
θ
+
3
π
)
)
2
sin
6
0
∘
=
3
r
2
cos
2
(
θ
+
3
π
)
A
r
e
a
o
f
b
i
g
t
r
i
a
n
g
l
e
=
2
1
r
2
sin
6
0
∘
=
4
3
r
2
A
r
e
a
o
f
b
i
g
t
r
i
a
n
g
l
e
A
r
e
a
o
f
s
m
a
l
l
t
r
i
a
n
g
l
e
=
4
3
r
2
3
r
2
cos
2
(
θ
+
3
π
)
=
4
cos
2
(
θ
+
3
π
)
So
α
=
4
and
β
=
3
, so the answer is 7.
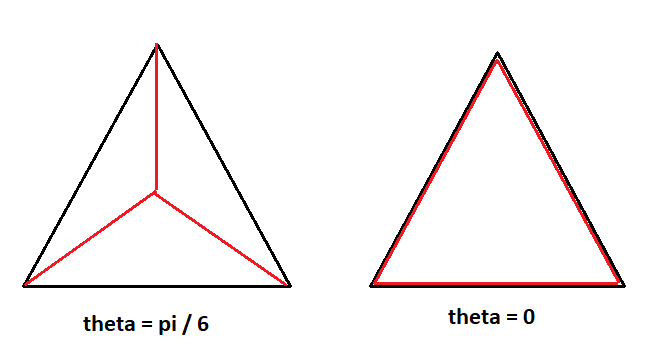
Here's a bit of a hacky solution. It's not complete because it assumes that the general form provided is correct. However, I think it's kind of nice.
When θ = 6 π , the area of the small triangle is zero:
⟹ c o s ( 6 π + β π ) = 0 ⟹ β = 3
When θ = 0 , the area of the small triangle is the same as the area of the big triangle:
⟹ α c o s 2 ( 3 π ) = 1 α 4 1 = 1 ⟹ α = 4